Atmospheric Humidity

Quantifying water vapor content in the atmosphere

Atmospheric Humidity

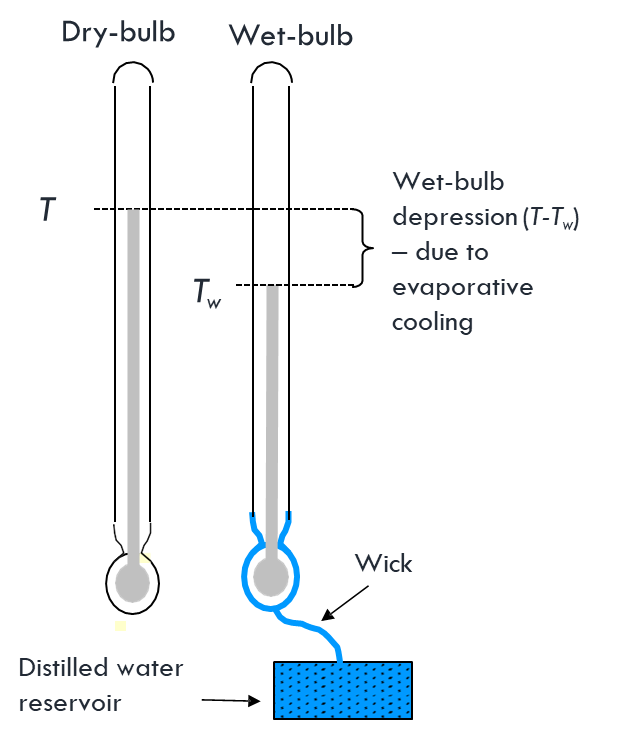
An Assmann Psycrhometer can be used to measure the wet bulb temperature and calculate atmospheric humidity

Learning objectives

  • Describe the physical and biological significance of atmospheric humidity
  • Define vapor density (or absolute humidity)
  • Be able to convert between vapor density and vapor pressure
  • Understand the relationship of saturation vapor density to temperature
  • Define and know how to calculate relative humidity
  • Know other important measures of humidity - vapor density deficit, vapor pressure deficit, dew point temperature & wet bulb depression
  • Give examples of sensors that can measure humidity

Atmospheric Humidity

Water vapor makes up small part of atmosphere, but has important physical and biological significance because:

  • It’s a major greenhouse gas
  • Plays a major role in energy transport globally and locally
  • Affects animal comfort, plant disease, fire weather, metal corrosion, etc.
Table 1: Approximate composition of the atmosphere.
Gas Proportion
Nitrogen (N2) 78.08%
Oxygen (O2) 20.95%
Argon (Ar) 0.93%
Carbon Dioxide (CO2) 0.04%
Misc. Trace Gasses <0.01%
Water Vapor (H2O) 0-3%

Atmospheric Humidity

  • The heat released by condensing 1 g of water is enough to raise 1 kg of air (0.8 m3) by 2.5 °C
    • Due to water’s very high heat of vaporization, 2450 J g-1
    • Freezing water releases another 330 J g-1
  • We feel cold after coming out of a swimming pool because the heat used for evaporation of the water comes from our skin

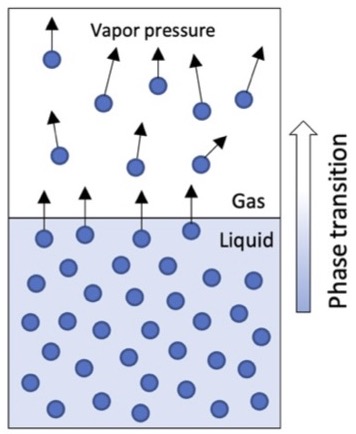
Vapor Density

Vapor density (\(\rho_v\)) is the mass of water vapor per unit volume of air (g m-3); it is the fundamental measure of humidity.

  • The ‘driving force’ for evaporation is the \(\rho_v\) gradient between an evaporating surface and the surrounding air.

Density is the mass of a substance per unit volume (e.g., 1 m-3)

Vapor Pressure

Vapor pressure (\(P_v\)) is the partial pressure (aka force) exerted by water vapor in a parcel of air.

  • A slightly more abstract measure of humidity.

  • Mean sea level air pressure is 101.325 kPa

  • \(P_v \leq 5 kPa\)

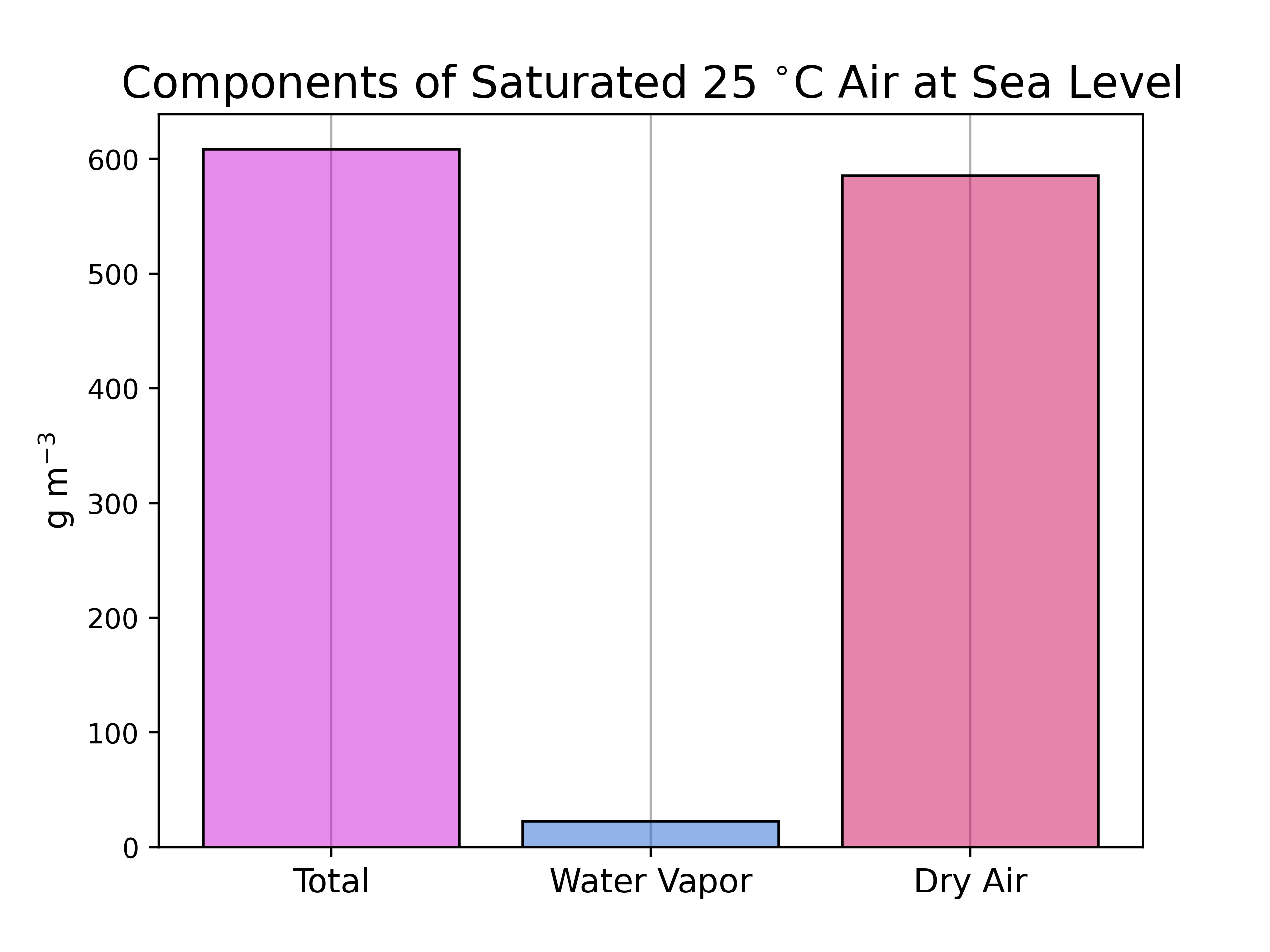
Mixing Ratio

Water vapor content can also be expressed as a mixing ratio, which gives the abundance of one component of a mixture (H2O) relative to all other components (“dry air”).

\(r_{H2O} = \frac{m_{H2O}}{m_{dry}}\) \(m_{dry} = m_{total} - m_{H2O}\)

  • Usually parts per thousand for water vapor
    • g H2O per kg dry air
  • In this example:

\(m_{dry} = 608.5 g - 23 g = 0.5855 kg\)

\(r_{H2O} = \frac{23 g}{0.5855 kg} = 39.28 \frac{g}{kg}\)

Ideal Gas Law

Describes the state of a gas as a function of pressure (\(P\)), volume (\(V\)), temperature (\(T\)) in Kelvin, the amount of the gas (\(n\)) in moles; and the ideal gas constant (\(R\) = 8.314 x 10 \(^{-3}\) kPa m \(^3\) g \(^{-1}\) K \(^{-1}\)).

\[ PV=nRT \qquad(1)\]

  • \(n = \frac{m}{M}\), where \(m\) is the mass of the substance and \(M\) is the Molar mass of the substance.
  • Can be applied to a mixture of gasses (e.g., dry air) or a single gas (e.g., water vapor)

Ideal Gas Law

The molar mass of water is 18.015 g mol \(^{-1}\). Given this, we can redefine Equation 1 in terms of \(\rho_v\) and \(P_v\) as Equation 2.

\[ \rho_v = \frac{P_vM}{RT} \qquad(2)\]

  • This allows us to convert between \(\rho_v\) and \(P_v\)
    • Knowing one, allows easy calculation of the other

Saturation

The ability of air to hold water vapor increases exponentially with temperature.

  • We add a “\(^*\)” to indicate saturation:
    • Saturation vapor density \(\rho_v^*\)
    • Saturation vapor pressure \(P_v^*\)

Laten Heat

Determining \(\rho_v^*\) or \(P_v^*\) for a given \(T\) requires integrating the Clausius–Clapeyron equation.

  • The latent heat of vaporization \(L\) is also varies as a function of \(T\)

\[ \frac{d P}{d T} = \frac{L P}{R T^2} \qquad(3)\]

Figure 1: Latent heat of evaporation / condensation at different temperatures

Saturation

Luckily, some experimentally based empirical relationships have been developed for typical conditions on Earth’s surface.

  • It turns out temperature (\(T\)) and pressure (\(P\)) changes have an equal and opposite effect on saturation pressure \(P_v^*\)
    • We can calculate \(P_v^*\) to \(\pm\) 0.1% for typical temperature conditions using the empirically derived Buck Equation:

\[ P_v^*=0.61121e^{(18.678-\frac{T}{234.5})(\frac{T}{257.14+T})} \qquad(4)\]

Saturation

Figure 2: Saturation vapor pressure \(P_v^*\) as a function of temperature \(T\)
Figure 3: Saturation vapor density \(\rho_v^*\) as a function of temperature \(T\)

Partial Saturation

Typically, ambient air is not saturated. An air parcel such as the one the figure can be brought to saturation by:

  • Adding moisture to the air
  • Cooling the air
Figure 4: Saturation vapor density \(\rho_v^*\) as a function of temperature \(T\)

Dewpoint temperature (Td)

The temperature down to which the air must be cooled isobarically (without changing air pressure) for it to become saturated.

Can be measured with a silver coated cooled mirror. \(T_d\) is the temperature of the mirror when water vapor condenses on it.

Dewpoint Calculation (iClicker)

You can determine \(T_d\) from \(\rho_v\) or \(P_v\) using the relationship between \(T\) and \(\rho_v^*\) or \(P_v^*\)

  • If \(T\) = 20 °C and \(P_v\) = 1.7 kPa, what is \(T_d\)?

    • A 20 °C
    • B 15 °C
Figure 5: Saturation vapor pressure \(P_v^*\) as a function of temperature \(T\)

Condensation

If an air parcel to cools below \(T_d\), condensation will* occur.

  • Condensation releases heat which warms the surrounding environment
    • Cloud formation is an important avenue of energy exchange
  • Condensation nuclei are required to initiate condensation.
    • In the absence nuclei, which can occur in the upper atmosphere, air will become supersaturated
    • Earth’s surface is a nuclei, so supersaturation doesn’t occur near the surface.

Relative Humidity

Humidity can be expressed as a fraction or % of the maximum (saturation) water vapor the air can hold at that temperature:

\[ RH = \frac{\rho_v}{\rho_v^*} \qquad(5)\]

  • RH depends on T because \(\rho_v^*\) is a function of T

Relative Humidity and Temperature

The variation in RH during the day is largely determined by the variation in temperature.

Air temperature and RH are usually in anti-phase

\(r_{H2O}\) stays same but \(T\) and \(RH\) change

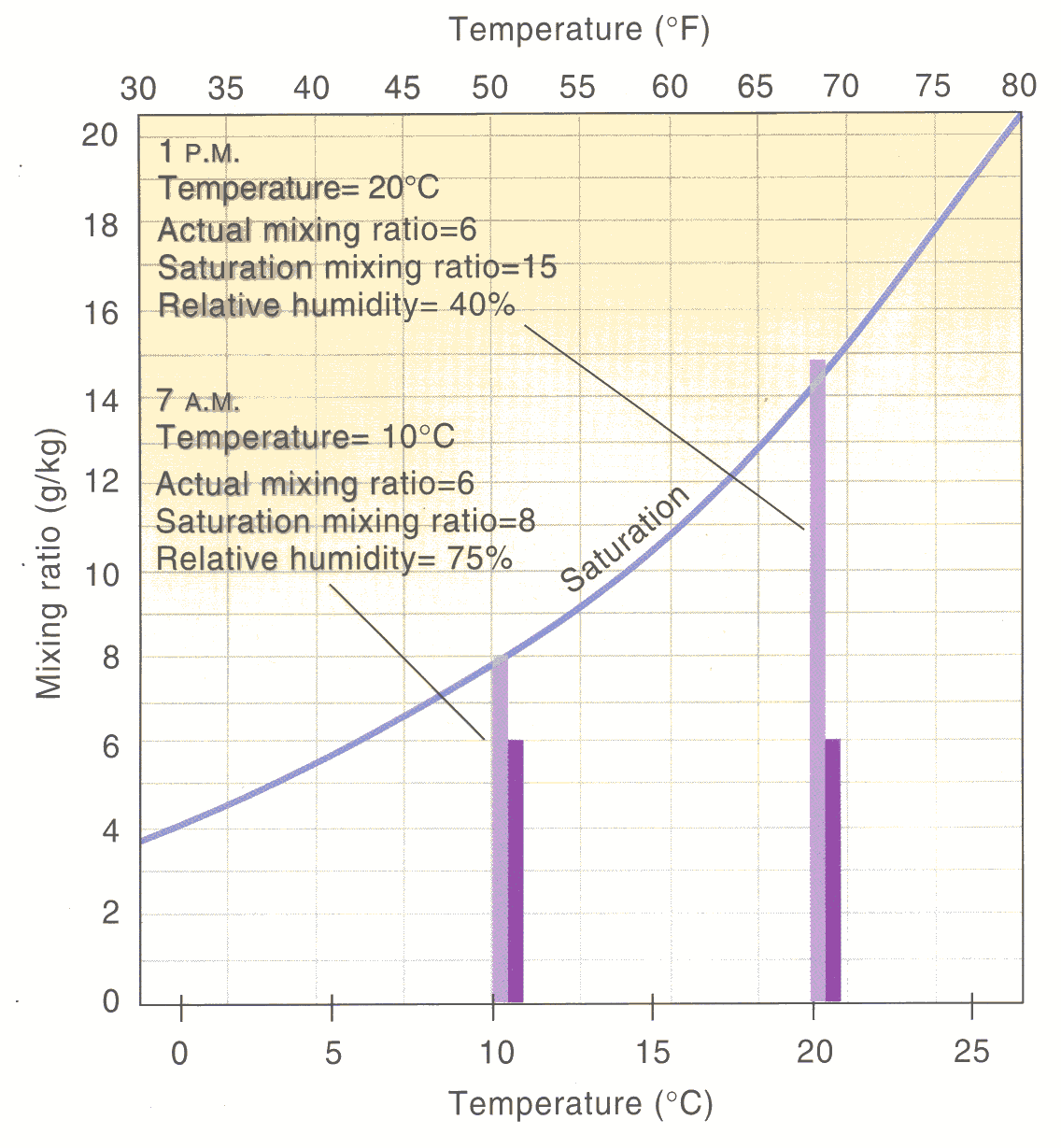
Importance of RH

  • Determines the water content of porous media e.g., wood, soil, clothing, which has been allowed to equilibrate with the air.
  • Low RH (< 30%) contributes to high risk of forest fire
  • Metal corrosion is directly related to RH.
  • Many plant diseases are strongly affected by RH.

Relative Humidity (iClicker)

In the classroom, T = 21°C and \(\rho_v\) = 9 g m-3. What is the RH?

  • A 5%
  • B 100%
  • C 25%
  • D 50%
Figure 6: Saturation vapor density \(\rho_v^*\) as a function of temperature \(T\)

Relative Humidity example

  • In the classroom, \(T\) = 21 °C and \(\rho_v\) = 9 g m-3. What is the RH?
    • First determine \(\rho_v^*\) using the graph. It is \(\approx\) 18 g m-3.
    • Then RH = \(\rho_v\) / \(\rho_v^*\) = (9/18) x 100% = 50%.

Vapor Density Deficit (VDD)

The increase in \(\rho_v\) necessary to bring the air to saturation It is expressed as:

\[ VDD = \rho_v^* - \rho_v \qquad(6)\]

  • RH doesn’t determine the rate of evaporation or condensation
    • The difference between vapor density at the exchange surface and the air determines it!

VDD (iClicker)

In the classroom, T = 21°C and \(\rho_v\) = 9 g m-3. We know that \(\rho_v^* \approx\) 18 g m-3. So What is the VDD?

\(VDD = rho_v^* - rho_v =\) 9 g m-3

Vapor Pressure Deficit (VPD)

This variable is very similar to VDD

\[ VPD = P_v^* - P_v \qquad(7)\]

  • Helpful to understand the response of the stomata of leaves to the dryness of the air

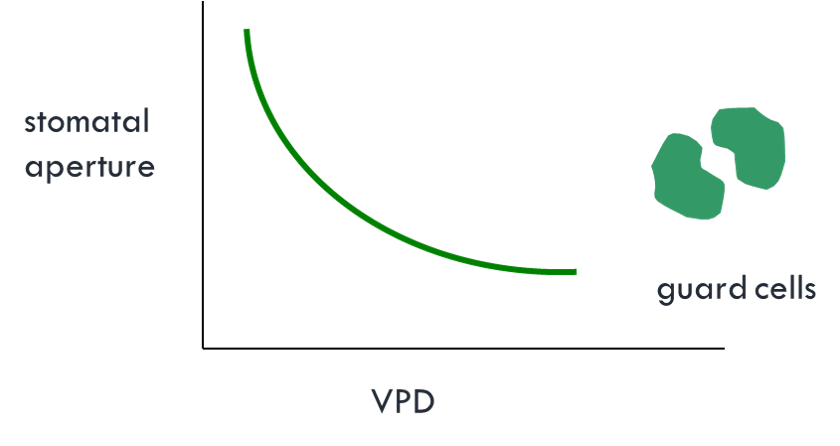
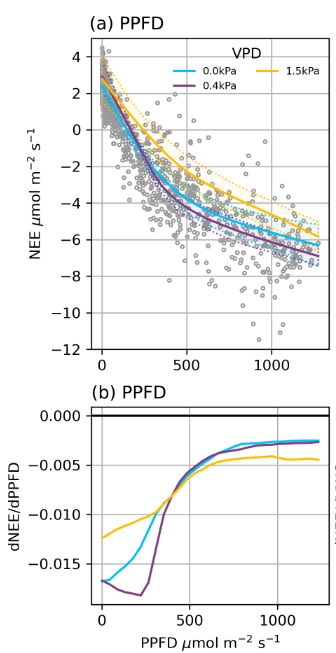
Vapor Pressure Deficit (VPD)

Rates of photosynthesis are influenced by VPD.

  • With increasing VPD, photosynthesis first becomes more efficient as the pressure gradient aids gas transfer between the leaves and the atmosphere
  • Then it has a strong limiting effect as plants close their stomata to avoid excess water loss

Measuring Humidity

  • RH has been measured by different methods: Leonardo de Vinci used the weight of a ball of wool.
  • de Saussure invented the hair hygrometer (2.5% change in length for 0 to 100% RH).
  • At fire weather stations, the weight of small sticks of wood has been used.
  • More recently changes in electrical conductivity resulting from adsorption of water vapor by a thin polymer film coated on small sensing chips has proven to be very effective.
    • These are commonly used in climate stations.

Measuring RH

Vaisala HMP35C probe with air filter

HMP35C with air filter removed showing RH sensing chip 

Psychrometry

  • The size of the depression is a measure of the rate of removal of latent heat
    • Which is due to the dryness of the ambient air relative to saturation at the temperature of the evaporating surface (the wet-bulb)

Infrared gas analyzer (IRGA) 

Fast-response IRGA using the absorption of near-infrared radiation by water vapor (or CO2) as the means of sensing humidity.

  • Used in the eddy-covariance method of measuring fluxes of water vapor
    • we’ll discuss later. 

Take home points

  • Makes up small part of atmosphere but is the main greenhouse gas 
  • Large latent heat of vaporization (conversion of liquid to vapor) 
  • Relationship of vapor density to vapor pressure by ideal gas law 
  • Saturation vapor density (ability of air to store water vapor) (v *) is exponentially related to temperature 
  • RH (v/v ) and VDD (v - v) are very sensitive to temperature 
  • vapor density difference determines rate of H2O vapor transfer 
  • RH determines equilibrium water content of porous materials such as fire fuels & affects animal comfort, plant disease & metal corrosion 
  • Leaf stomata close as VDD or VPD increases 

Back to Homepage