Orographic Lift

How is the atmosphere organized and how do key properties of the atmosphere vary through out it

Learning Objectives

  • Understand how adiabatic processes effect temperature and moisture conditions British Columbia

The Adiabatic Process Equation

To determine how the temperature of a parcel (\(T_p\)) will change adiabatically if it is transported between two height levels (\(z_1\) & \(z_2\)), given \(T_p(z_1)\) and \(T_{dp}(z_1)\):


\[ T_p(z_2) = \begin{cases} T_p(z_1) + min((LCL-z_1),(z_2-z_1)) * DALR + max(z_2-LCL,0) * SALR \ , \text{if} z_2>z_1 \\ T_p(z_1) + (z_2-z_1) * DALR \ , \text{if} z_1>z_2 \end{cases} \qquad(1)\]

  • Assume DALR = -0.01 K m-1 SALR = -0.005 K m-1
  • Recall: \(\frac{T_{dz_1}-T_{z_1}}{DALR}+z_1\)

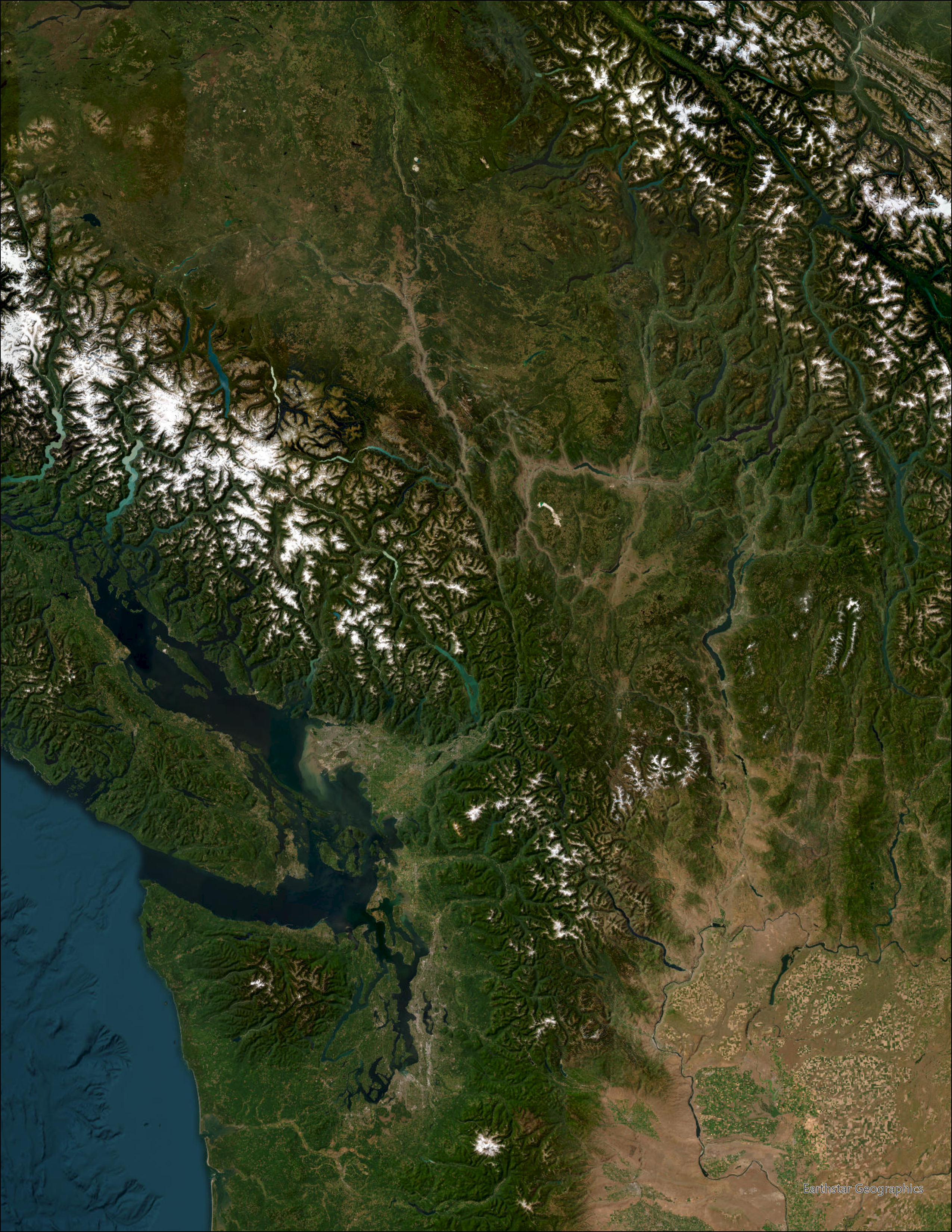
Orographic Lift

When air from low elevations is forced up a slope.

  • A common occurrence in BC during the winter

    • Moist air from the Pacific Ocean collides with Coast Mountains

  • Often results in precipitation on the “windward” side of mountains

    • As air rises it cools, reaching saturation

Orographic Lift

Largely responsible for maintaining the temperate rain forests of our region.

  • Many of the wettest locations in the world:
    • Winds consistently push moist ocean air up mountain slopes

The Rain Shadow Effect

Also responsible for the desert like climate of the Okanagan Valley.

  • Despite it’s its proximity to the coast, dry hot winds are a persistent in this region

  • Many of the driest locations in the world are in the “rainshadow” of large mountain ranges

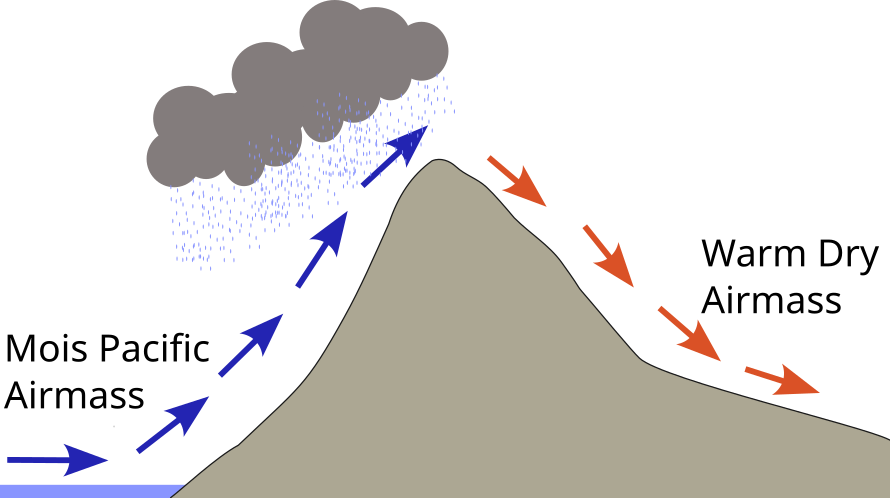
The Mountain Problem

This is classic example of these phenomena in Meteorology. Given \(T\) and \(T_d\) at the base of a mountain:

  • Determine the \(LCL\)
  • Estimate how \(T\) and \(T_d\) will evolve as air moves up and over a mountain

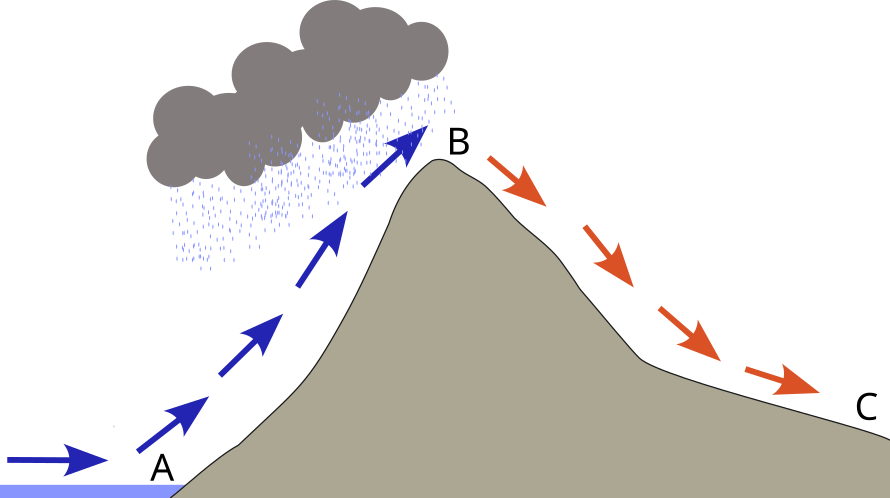
The Mountain Problem

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

Step 1: Determine the LCL

T_A = 10
Td_A = 8
z_A = 0
DALR = -0.01
SALR = -0.005

LCL = (Td_A - T_A)/DALR+z_A

LCL = 200 m.a.s.l

The Mountain Problem (iClicker)

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

What will \(T\) be at the LCL?

  • A. \(T = 10 ^{\circ}C\)
  • B. \(T = 9 ^{\circ}C\)
  • C. \(T = 8 ^{\circ}C\)
  • D. \(T = 7 ^{\circ}C\)

The Mountain Problem

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

Step 2: Evaluate the Adiabatic Process Equation for B

The Mountain Problem

z_B = 2500

T_B = T_A + min((LCL-z_A),(z_B-z_A))*DALR + max(z_B-LCL,0)*SALR

Step 2: Evaluate the Adiabatic Process Equation for B

\(T\) at B = -3.5 \(^{\circ}\)

The Mountain Problem (iClicker)

z_B = 2500

T_B = T_A + min((LCL-z_A),(z_B-z_A))*DALR + max(z_B-LCL,0)*SALR

What will \(T_d\) be at B?

  • A. \(T_d\) = -3.5 \(^{\circ}\)
  • B. \(T_d\) = 10 \(^{\circ}\)
  • C. \(T_d\) < -3.5 \(^{\circ}\)
  • D. \(T_d\) > -3.5 \(^{\circ}\)

The Mountain Problem (iClicker)

Given \(T\) = -3.5 \(^{\circ}\) and \(T_d\) = -3.5 \(^{\circ}\) at B, do you think precipitation will be occurring at B?

What will \(T_d\) be at B?

  • A. Yes, it will probably be snowing
  • B. Yes, it will probably be raining
  • C. Probably not

The Mountain Problem

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

Step 3: Evaluate the Adiabatic Process Equation for C

z_C = 300

T_C =T_B + (z_C-z_B)*DALR

\(T\) at C = 18.5 \(^{\circ}\)

The Mountain Problem (iClicker)

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

What will \(T_d\) be at C?

  • A. \(T_d\) = 8 \(^{\circ}\)
  • B. \(T_d\) = 18.5 \(^{\circ}\)
  • C. \(T_d\) = -3.5 \(^{\circ}\)
  • D. Not enough information to know

Putting it all Together

I’m going to show you how you can evaluate the adiabatic process equation (APE) in R. If you’d like to try it out yourself, you can install R on your computer and try it out.

  • You can find the materials need here
    • You can use R studio to evaluate the APE on quizzes/exams if you want
    • Totally not mandatory! You can do it by hand too.

Putting it all Together

# Evaluating the adiabatic process equation (APE) in R

# A "Class" can contain values with variables (e.g., T, TD, and z)
setClass(Class="Parcel",representation(T="numeric",Td="numeric",z="numeric"))

# A function can evaluate an equation repeatedly given different inputs
APE <- function(Parcel,z2){
  DALR = -0.01
  SALR = -0.005
  # Calculate the LCL
  LCL = (Parcel@Td-Parcel@T)/DALR+Parcel@z
  # Evaluate the APE and update the parcel temperature
  Parcel@T = Parcel@T + min((LCL-Parcel@z),(z2-Parcel@z))*DALR + max(z2-LCL,0)*SALR
  # Update the parcel's height and dewpoint if necessary
  Parcel@z=z2
  if(Parcel@z>=LCL){Parcel@Td = Parcel@T}
  return(Parcel)
}

Putting it all Together

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

# Define the Parcel at A
A = new("Parcel",T=10,Td=8,z=0)
A
An object of class "Parcel"
Slot "T":
[1] 10

Slot "Td":
[1] 8

Slot "z":
[1] 0

Putting it all Together

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

# Evaluate APE for B
B = APE(A,2500)
B
An object of class "Parcel"
Slot "T":
[1] -3.5

Slot "Td":
[1] -3.5

Slot "z":
[1] 2500

Putting it all Together

At A: \(z = 0 \ m\), \(T = 10 ^{\circ}C\), and \(T_d = 8 ^{\circ}C\). What will \(T\) and \(T_d\) be at B (\(z = 2500 \ m\)) and C (\(z = 300 \ m\))?

# Evaluate APE for B
C = APE(B,300)
C
An object of class "Parcel"
Slot "T":
[1] 18.5

Slot "Td":
[1] -3.5

Slot "z":
[1] 300

Take home points

  • Temperature decreases with height on the windward slope of a mountain
    • Condensation/Precipitation will often occur
  • Temperature increases as winds move down the leeward slope of a mountain
    • \(RH\) decreases as well, because \(T_d\) remains unchanged while \(T\) increases

Back to Homepage