Radiation Laws

The earth climate and ecosystems are driven by radiation emitted by the sun.

Learning Objectives

• Understand exactly what is radiation and why it is relevant in biometeorology & climate science.
• Describe the quantity and quality of radiative energy.
• Know which physical laws can be used to predict quantity and characteristics of radiation emitted.

Radiation Laws

An solar flare erupting on Sun as seen from SOHO (Solar and Heliospheric Observatory)

Sunlight passing through a forest canopy

In order to lay the groundwork and foundation for what is to come in the course we need to understand some basics regarding temperature and energy

Radiation is emitted from all matter

GEOB 200 / APBI 244 students emit radiation!

We have all seen thermal infra-red imagery! ALL OBJECTS above absolute zero temperature emit radiation. The amount of radiation, and the wavelengths of that radiation are a function primarily of TEMPERATURE.

Characteristics of Radiation

It is the emission of energy as electromagnetic waves or as moving particles.

• Can travel in a vacuum (space).
  • Travels in straight lines at up to \(c = 3 * 10^{8} m s^{-1}\)
    • Takes 8 min 20 s to travel from the Sun to the Earth.

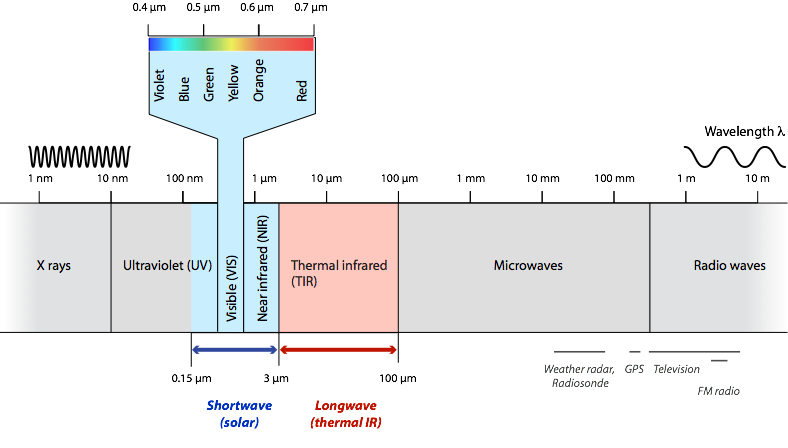
The electromagnetic spectrum

The radaition coming from the sun (solar radiation) is part of spectrum of electromagnetic radiation that includes X-rays, microwaves, radio waves etc. Our eyes are adapted to see a large portion of that solar radiation which we call “visible” light. Each colour that we see is associated with a particular wavelength of solar radiation. Green light for example has a wavelength of approximately 0.5 micrometers (millions of a meter).

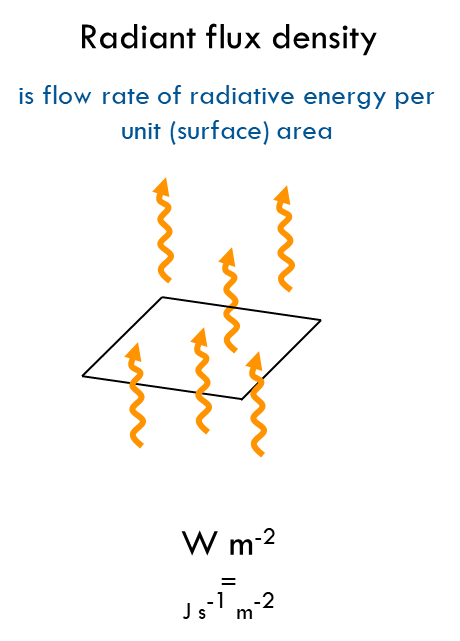
Radiant flux density

This a reminder from the previous lecture. We will use the term Wm-2 extensively through this class. It denotes the amount of energy (in this case radiative energy) passing through a square meter every second.

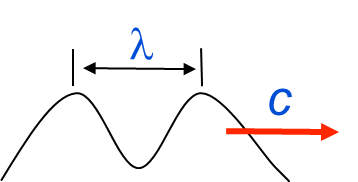
Wave-like

• Wavelength \(\lambda\) (m) & frequency \(ν=\frac{c}{\lambda}\)
  • c is the speed of light.

\[ v=\frac{c}{\lambda} \qquad(1)\]

Particle-like

• Energy emitted in discrete packets (Photons)
• Energy of a photon
• Planck’s constant: \(h = 6.63 * 10^{-34} J s\)

\[ e = hv \qquad(2)\]

Physicists tend to think of the behaviour of waves in two different ways. The first is to describe them as have a frequency and wavelength (just like waves in the ocean). The other is to view radiation of being like Particles, that is being discrete packets of energy or photons.

Energy content of a photon (iClicker)

What is the energy content (\(e\)) of one photon of yellow light (\({\lambda} = 0.55 \mu m\))?

\(v=\frac{c}{\lambda}\)

\(e=hv\)

• Note:
  • \(c = 3 * 10^{8} m s^{-1}\)
  • \(h = 6.63 * 10^{-34} J s\)
  • \(1 \mu m = 10^{-6} m\)

• A: \(3.6 x 10^{-19} J\)
• B: \(4.1 x 10^{45} W\)
• C: \(0.1 x 10^{-3} s^{-1}\)
• D: \(10.1 x 10^{5} m^{2}\)

Energy content of a photon (iClicker)

What is the energy content (\(e\)) of one photon of yellow light (\({\lambda} = 0.55 \mu m\))?

\(v=\frac{c}{\lambda}\)

\(e=hv\)

• Note:
  • \(c = 3 * 10^{8} m s^{-1}\)
  • \(h = 6.63 * 10^{-34} J s\)
  • \(1 \mu m = 10^{-6} m\)

A: \(3.6 x 10^{-19} J\)

\(v = \frac{3 * 10^{8} m s^{-1}}{6.63 * 10-34 J s}\)

\(v = 5.5 * 10^{14} s^{-1}\)

\(e = 6.63 * 10^{-34} J s * 5.5 * 10^{14} s^{-1}\)

\(e = 3.6 * 10^{-19} J\)

This is not absolutely necessary but for those of you with a mathematical bent, here is an example calculation of frequency and energy associated with yellow light.

Why does it mater?

The calculation is important for photosynthesis. Plants respond to the number of photons they absorb rather than simply to the total energy absorbed.

• Plants can only use photons in the visible range of the spectrum
  • This region is also called photosynthetically active radiation (PAR)

We will talk a lot about PAR later in the course. Keep this idea in mind

Radiation vs. Temperature

Wien’s displacement law

The wavelength of maximum emission (\(\lambda_{max}\)) from an object is inversely proportional to the temperature T (in K) of its surface:

\[ \lambda_{max} = \frac{b}{T} \qquad(3)\]

• A general approximation for a ‘blackbody’
• b ≈ 2898 μm K

Wien’s displacement law

Can be used to determine T of an object without having to measure the flux density of emitted radiation.

• As \(T \uparrow\) >> \(λ_{max} \downarrow\)
  • A hot iron:
  • Dull red > bright red > orange > yellow > white
• Wavelength of red is longer than that of yellow

Short-wave vs. Long-wave

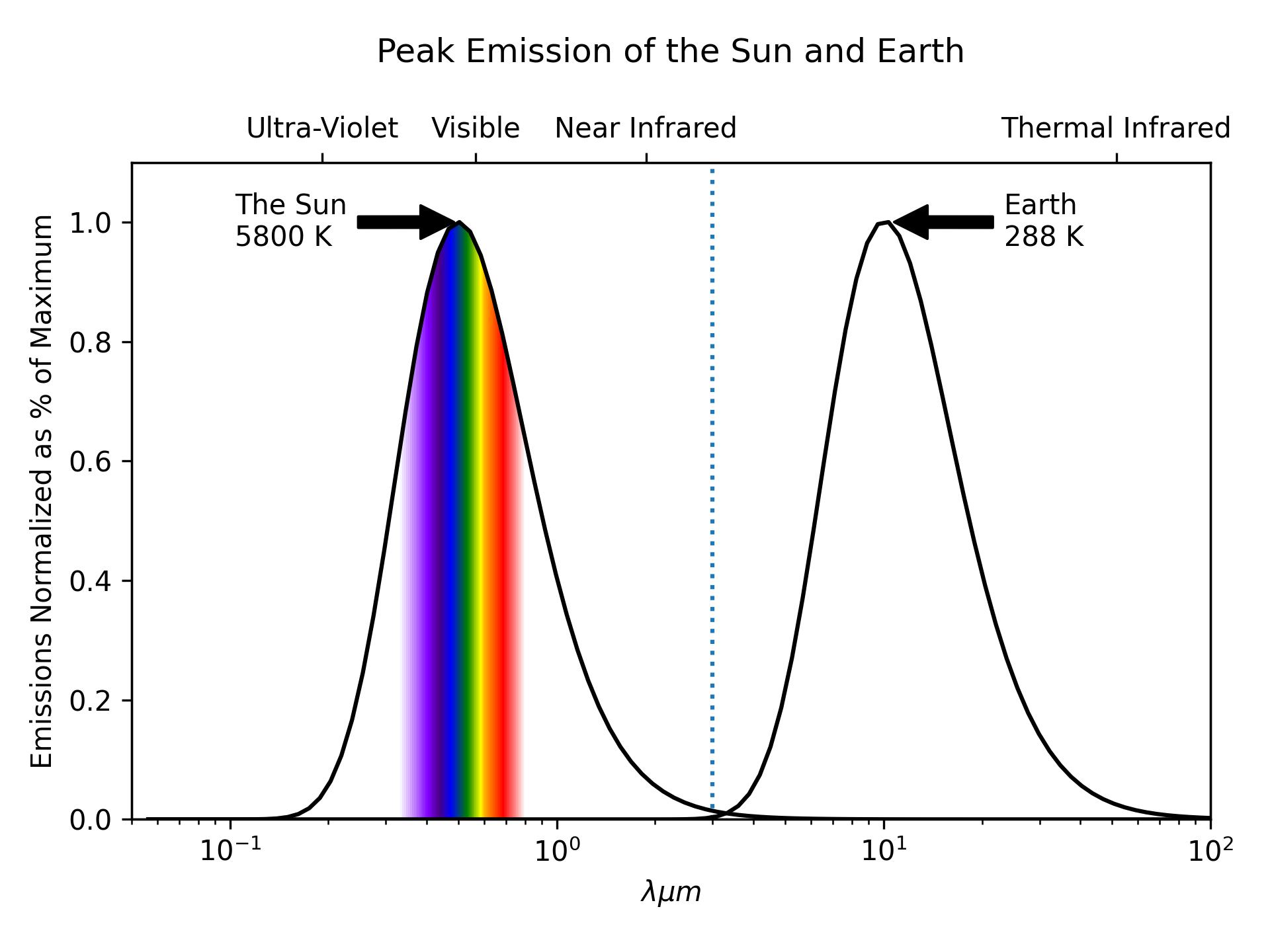
Short-wave vs. Long-wave

The exact boundary will vary from source to source; \(\lambda = 3 \mu m\) will be where we draw the distinction.

• Short-wave:
  • Higher energy radiation from the sun
• Long-wave:
  • Lower energy thermal radiation

Your peak emissions (iClicker)

The human body temperature is typically around 37 \(^{\circ}\) C, which is 310.15 K. What would the wavelength (\(\lambda\)) of a typical human’s peak emissions be (in \(\mu m\)) following Wein’s Law?

• \(\lambda_{max} = \frac{b}{T}\)
• \(b ≈ 2898 \mu m K\)

\(\lambda_{max} = \frac{2898 \mu m K}{310.15 K} = 9.34 \mu m\)

Stefan-Boltzmann law: blackbody

The total energy emitted by a blackbody \(Eb\) (emittance) is proportional to fourth power of its absolute Temperature:

\[ E_b = \sigma_b T^4 \qquad(4)\]

• \(\sigma_b = 5.67 * 10^{-8} W m^{-2}K^{-1}\)

  • \(\sigma_b\) is easy to remember
  • “5, 6, 7, 8”

Grey bodies

Emission from natural objects is given by adjusting the Stefan-Boltzman Law to account for surface emissivity (\(\epsilon\)).

• Emissivity is the ratio of the actual emission to that of a blackbody (\(\epsilon\) = 1.0).

\[ E_g = \epsilon\sigma_b T^4 \qquad(5)\]

Table 1: Emissivity of natural surfaces

Surface	X epsilon
Soil	0.90 – 0.98
Grass	0.90 – 0.95
Crops	0.90 – 0.99
Forests	0.97 – 0.99
Water	0.92 – 0.97

A black body is one that absorbs all the EM radiation (light…) that strikes it. To stay in thermal equilibrium, it must emit radiation at the same rate as it absorbs it so a black body also radiates well

Stefan-Boltzman Applications

The the basis of remote sensing in thermal satellite sensors and infrared thermometer use it to measure the surface temperature of objects

This approach is an inversion of the Stefan-Boltzmann law. That is the instrument measures the energy emitted from your forehead (the energy heats a little sensor in the infrared thermometer) and then knowing your emissivity, you can derive the temperature of your body

Total Emissions

Building on Wein and Stefan-Boltzman, we can use Plank’s law to calculate the total emissions from a body across the electromagnetic spectrum.

\[ E = \frac{2*h*c}{\lambda^{5}}*\frac{1}{e^{\frac{h*c}{\lambda*\sigma_b*T}}-1} \qquad(6)\]

• \(\sigma_b = 5.67 * 10^{-8} W m^{-2}K^{-1}\)
• \(c = 3 * 10^{8} m s^{-1}\)
• \(h = 6.63 * 10^{-34} J s\)

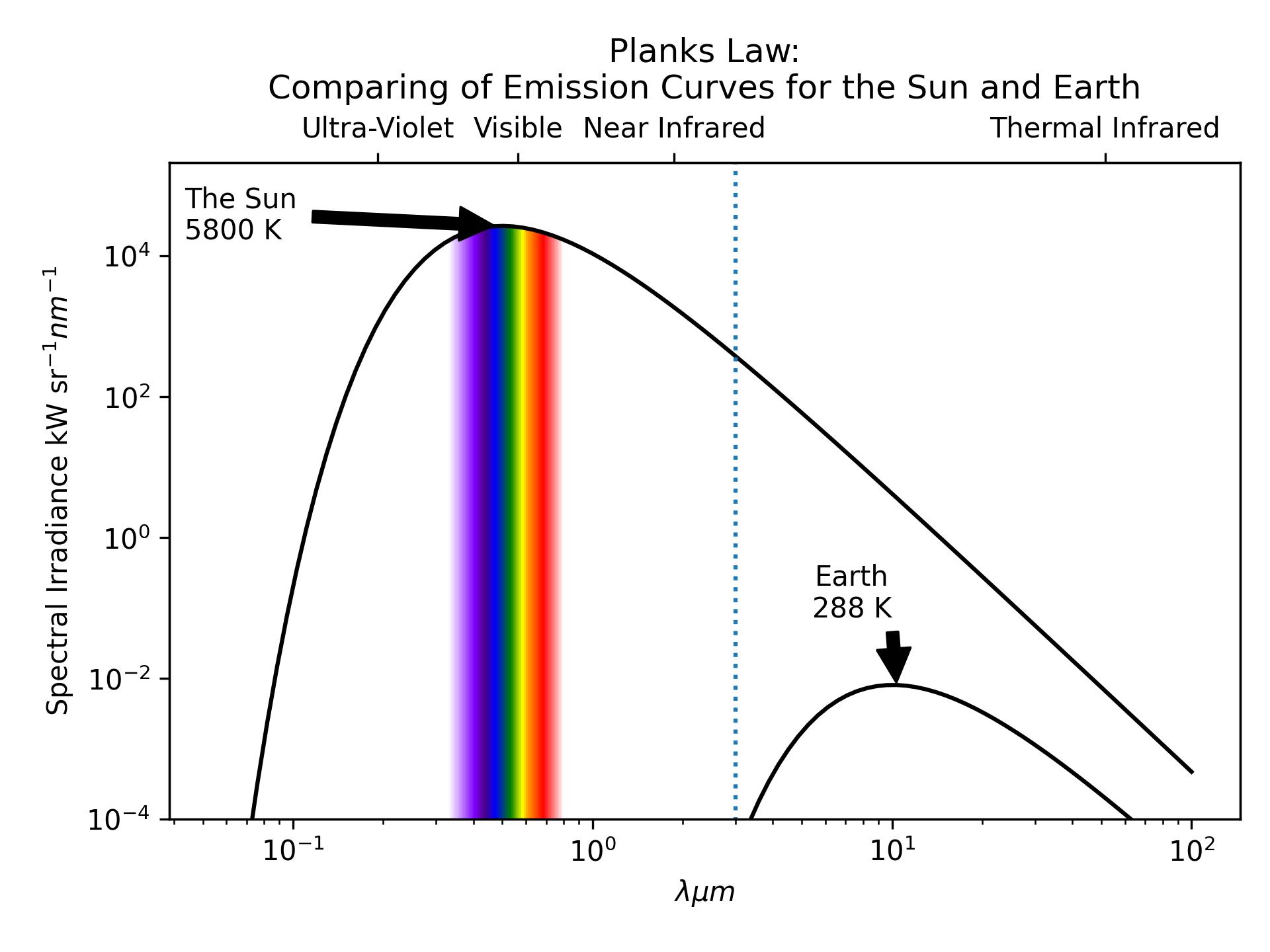
Total Emissions

Note the log scale. At their respective peaks the Sun’s emissions are \(10^{6}\) greater than the Earth’s.

• The Sun emits more radiation than the Earth
  • Across all wave lengths.

Radiation Balance

Radiation (of wavelength \(\lambda\)) can interact with an object in three ways:

• Absorption \(a_{\lambda}\)
• Transmission \(\tau_{\lambda}\)
• Reflection \(\alpha_{\lambda}\)

\[ a_\lambda + \tau_\lambda + \alpha_\lambda = 1 \qquad(7)\]

• These terms vary by object and by \(\lambda\), but all radiation reaching an object must be absorbed, transmitted, or reflected.

Absorption Spectra

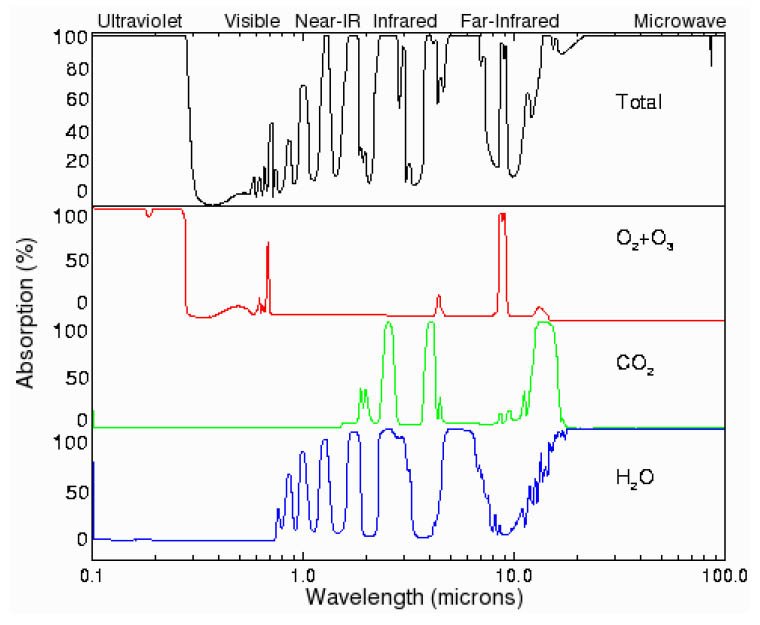
Absorption Spectra of Gasses in the Atmosphere

Reflection and Transmission

Whatever isn’t absorbed, must be either reflected, or transmitted.

• Liquid water transmits visible light well
  • It absorbs very little visible radiation
  • And it reflects very little too

Absorption Spectra of Liquid Water

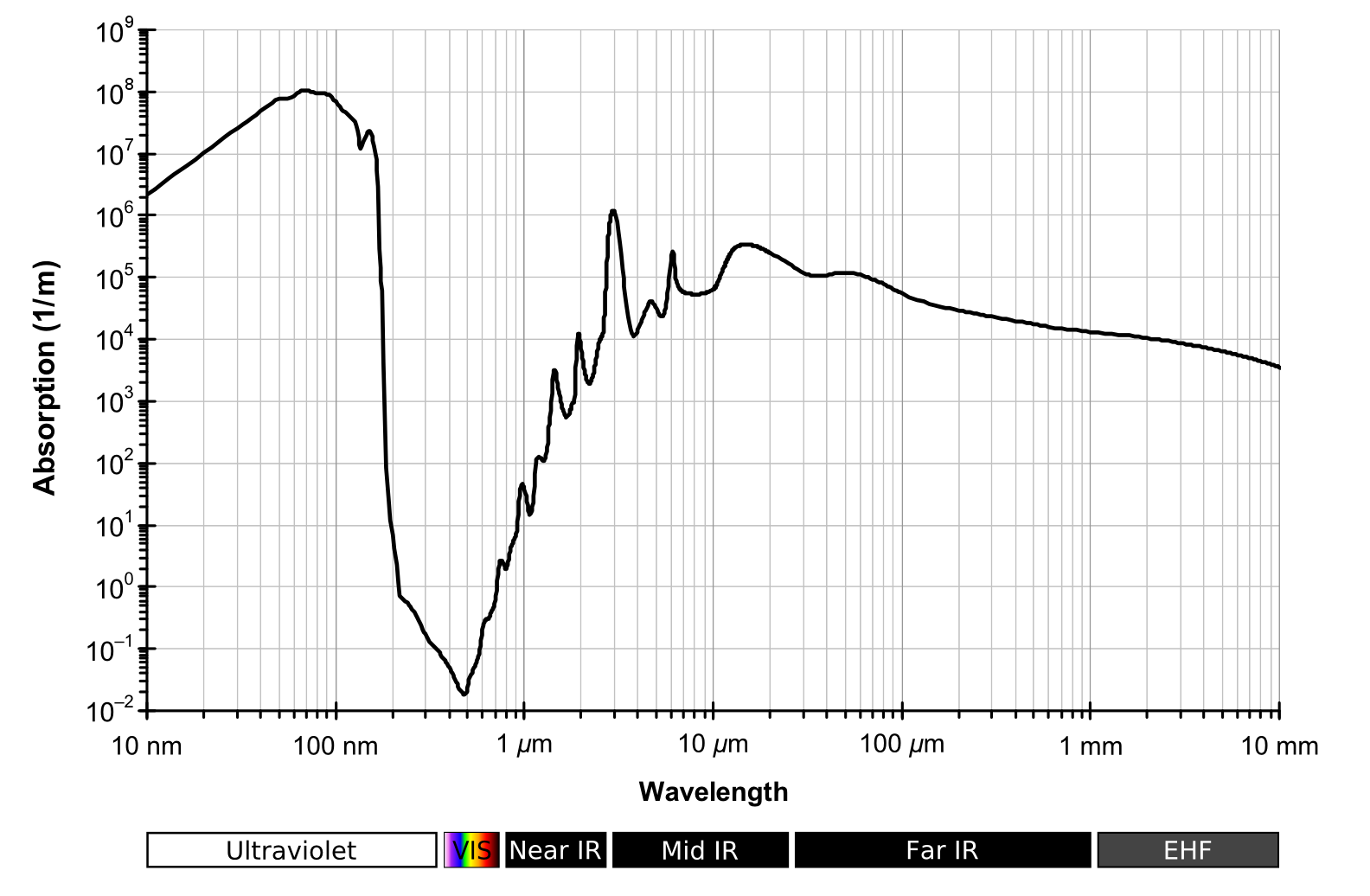
Accounting for reflectivity

Assuming the object isn’t transmissive (\(\tau \approx 0\)), which is the case for large objects like the earth across all but the longest wavelengths: \(a_{\lambda} + \alpha_{\lambda} = 1\)

• We can extend Stefan-Boltzman to account for reflectivity.

\[ E_g = \epsilon\sigma_b T^4 + (1-\epsilon) * (SW\downarrow+LW\downarrow) \qquad(8)\]

Net Radiation

Given this understanding, we can define Net Radiation (\(R_n\)) as the sum of all incoming (\(\downarrow\)) and outgoing(\(\uparrow\)) radiation components. We will specifically distinguish between short-wave (SW) and long-wave(LW) radiation.

\[ R_n = (SW \downarrow - SW \uparrow) + (LW \downarrow - LW \uparrow) \qquad(9)\]

Take home points

• What is the difference between long-wave and short-wave radiation?
• Know the the basic radiation laws: Wien’s Law, Stefan Boltzmann Law, and Plank’s law
  • These are idealized for black bodies, but can be modified.
• Radiation can be: absorbed, transmitted, or reflected.