Surface Geometry and Albedo

How incoming radiation interacts with surfaces

Learning Objectives

• Describe how is solar radiation distributed globally.
• Understand what happens when solar radiation reaches the ground or objects.
• Describe the process of reflection
  • Reflectivity and surface albedo
• Examples of controls on surface albedo.

Measuring reflectance with a pyranometer

Surface geometry and albedo

The reflectivity of water greatly changes depending on the sun’s positing

Temporal and spatial variation

Each of these factors effects incoming short-wave radiation:

• The Earth is a sphere (latitude)
• The Earth is tilted on its axis (seasons)
• The Earth rotates (time of day)
• The Earth has an atmosphere (absorption & scattering)
• The Earth’s surface is not flat

This is a really fundamental lecture that helps us understand the distribution of solar radiation on Earth and how ultimately this affects climate and the circulation (winds) on earth.

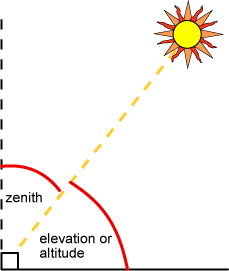
Defining the Solar Zenith

The local solar zenith (\(\theta\)) is the inverse of the local sun angle (\(\theta = 90 - sun\:angle\)). It varies globally as a function of season (solar declination) and locally as a function of latitude and time of day.

• At solar noon: the \(\theta\) reaches its daily minimum

\[ \theta = Latitude - Solar\:Declination \qquad(1)\]

• At sunrise/sunset the \(\theta = 90 ^{\circ}\)
• At other times of day it will fall between these values
• You can use this solar calculator time/date & location

Latitude

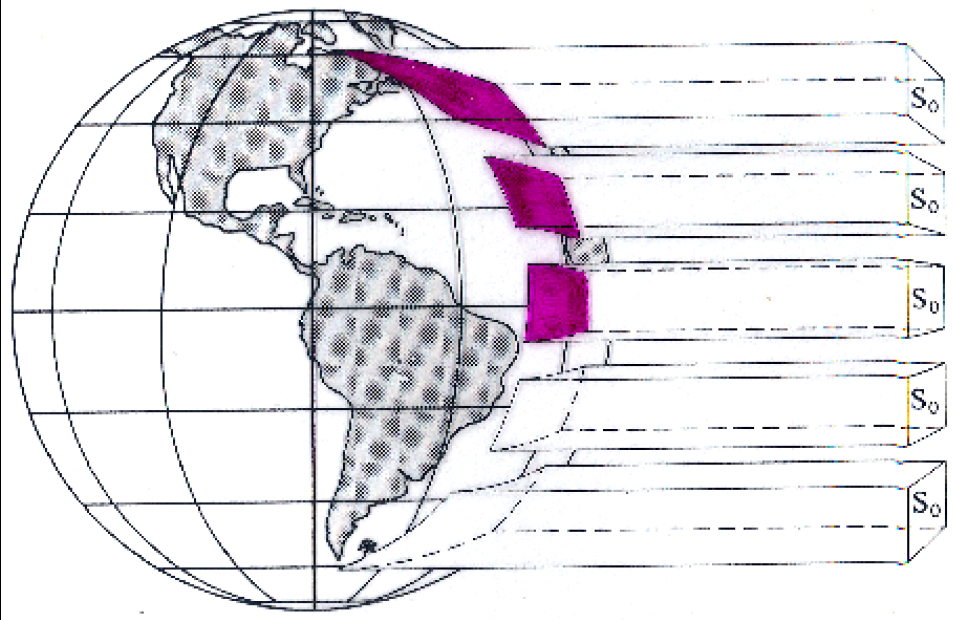
The effect of latitude is most obvious at the equinoxes, when Sun is overhead at the Equator.

Irradiance (at top of atmosphere) follows the Cosine law law of illumination:

\[ R_s = R_p cos(\theta) \qquad(2)\]

Table 1: Decrease of R_s with solar declination.

θ	Rs
0°	1.00 I0
23.5°	0.92 I0	8 % less
50°	0.64 I0	36 % less
80°	0.17 I0	83 % less

Think back to our discussion of the Cosine Law of Illumination. Again you try this with a flashlight and a globe or ball. Note that on the lower left globe S0 is the solar constant. By “extra-terrestrial” in this case we mean at the outer edge of the atmosphere (not aliens!)

Seasons

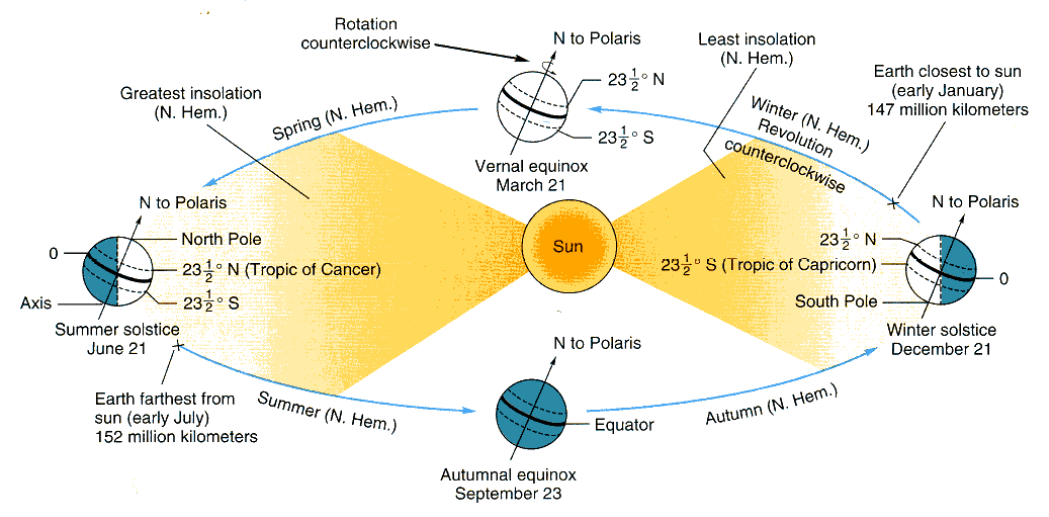
Effect of seasons - Earth’s tilt and orbit

This is the diagram that explains our seasons. Our rotating (once per day) planet is tilted at 23.5 degrees, and importantly, that tilt and its orientation is maintained as the earth follows it’s elliptical orbit (once per year). That tilt is what defines the Arctic and Antarctic circles (66.5o = 90o-23.5o), and is the reason that at winter solstice, areas north of the artic circle in the Northern hemisphere have 24 hours of darkness (likewise in the southern hemisphere 6 months later)

Season: Average daily input

• The tropics have high input (on average)
  • Less seasonal variation
• Higher latitudes have high input (on average)
  • Highest summer values

This is what the impact of the earth’s tilt has on radiation received at different latitudes.

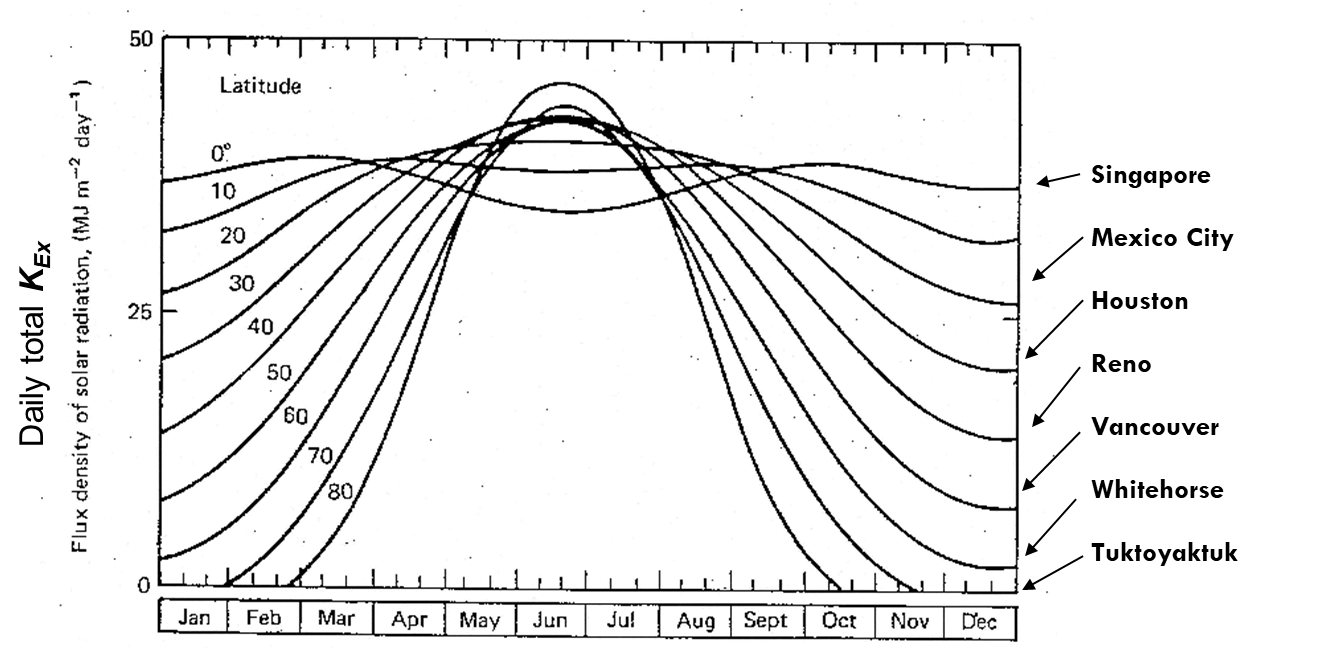
Time of Day

The local solar zenith (\(\theta\)) varies through the day as the earth rotates.

This is the SUN PATH diagram and shows where the sun appears in the sky by time for different times of year. Go outside now and see where the sun is. https://gml.noaa.gov/grad/solcalc/azel.html

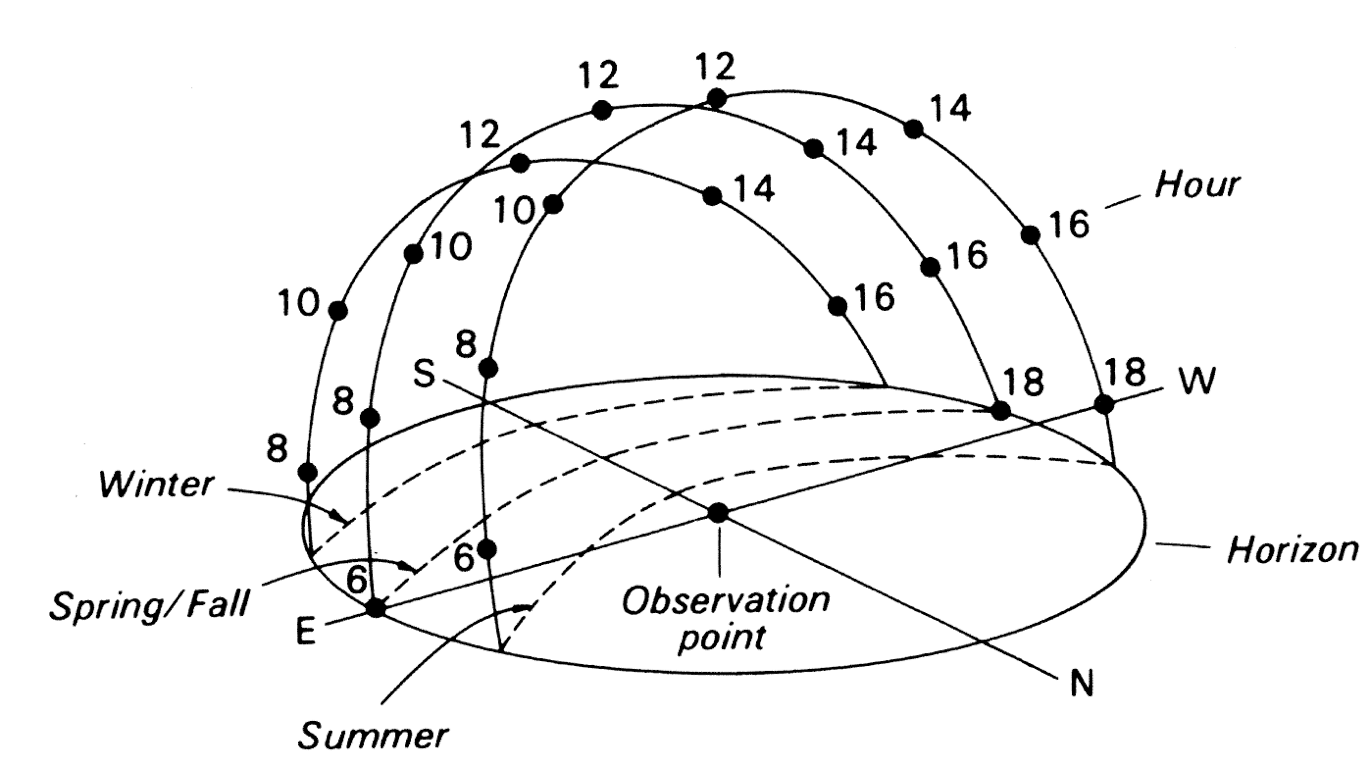
Diurnal Variation

With no clouds this gives a simple daily symmetry, like a sine curve.

Burns Bog Station, Delta, BC

Figure 1: Radiation data from the Burns Bog Flux Station June 29th, 2021.

This is the classic diurnal (sine wave like) variation in solar radiation as seen here south of Vancouver. The peak radiation flux density occurs around mid day (what we call solar noon) – remember the position of a place with respect to time zones may mean that solar noon is NOT at midday/noon.

Irradiance at Burns Bog (iClicker)

Which of these answers explains (in part) why observed incoming short-wave radiation at the Burns Bog station on June 29th, 2021 shown on the previous slide was less than the solar constant (\(I_0\))?

• A Reflection of solar radiation by clouds
• B Spreading of the solar beam (cosine law of illumination)
• C Both A & B

Recall

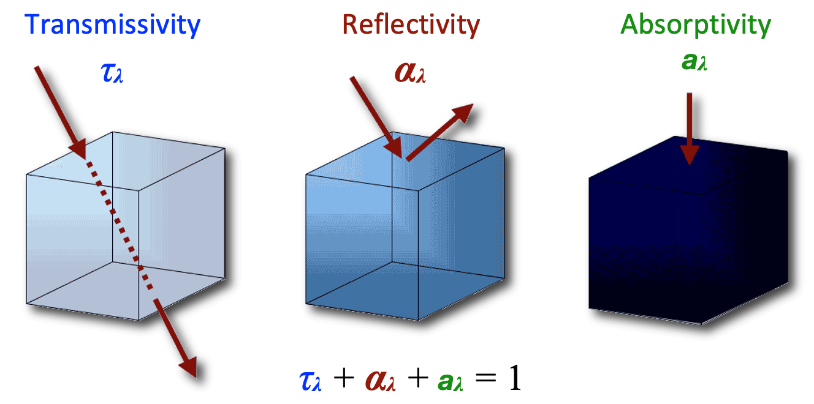
Radiation Balance: radiation (of wavelength \(\lambda\)) can interact with an object in three ways:

• Absorption \(a_{\lambda}\)
• Transmission \(\tau_{\lambda}\)
• Reflection \(\alpha_{\lambda}\)
  • For short-wave radiation, we use the term Albedo

\[ a_\lambda + \tau_\lambda + \alpha_\lambda = 1 \qquad(3)\]

Key Terms

Irradiance: flux density of incoming shortwave radiation on receiving horizontal surface (W m^-2)

Reflectance: flux density of reflected shortwave radiation the surface (W m^-2)

Albedo: proportion of irradiance that is reflected (unitless)

Measuring Albedo (iClicker)

Which instrument in this photo (A or B) would you use to measure reflectance?

Observations from Burns Bog

Figure 2: Irradiance and Reflectance at Burns Bog June 29th, 2021.

Figure 3: Irradiance and Reflectance at Burns Bog December 31st, 2021.

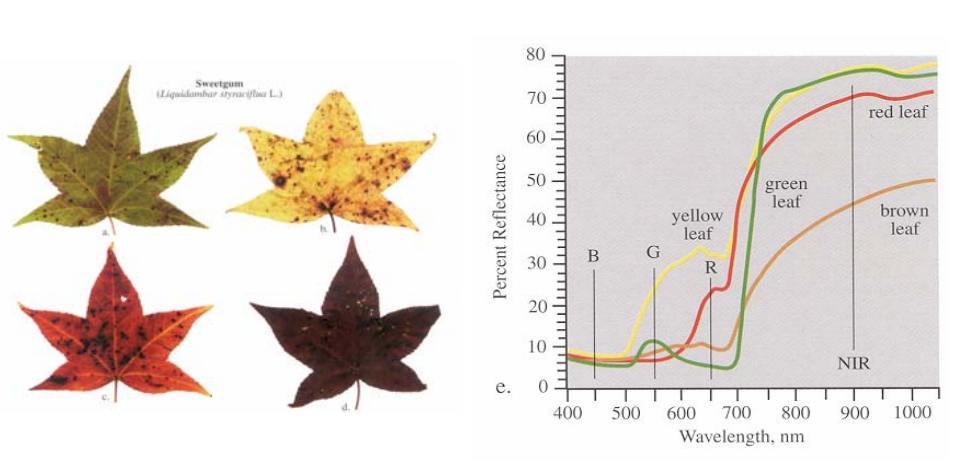
Spectral Reflectivity \(\alpha_{\lambda}\)

Leaves, soils, and rocks all have distinctive features.

• For opaque objects (e.g., rocks and soils) the spectral absorptivity is:

\[ a_{\lambda} = 1 - \alpha_{\lambda} \qquad(4)\]

• For transparent objects (e.g., leaves and water) the spectral absorptivity is:

\[ a_{\lambda} = 1 - \alpha_{\lambda} - \tau_{\lambda} \qquad(5)\]

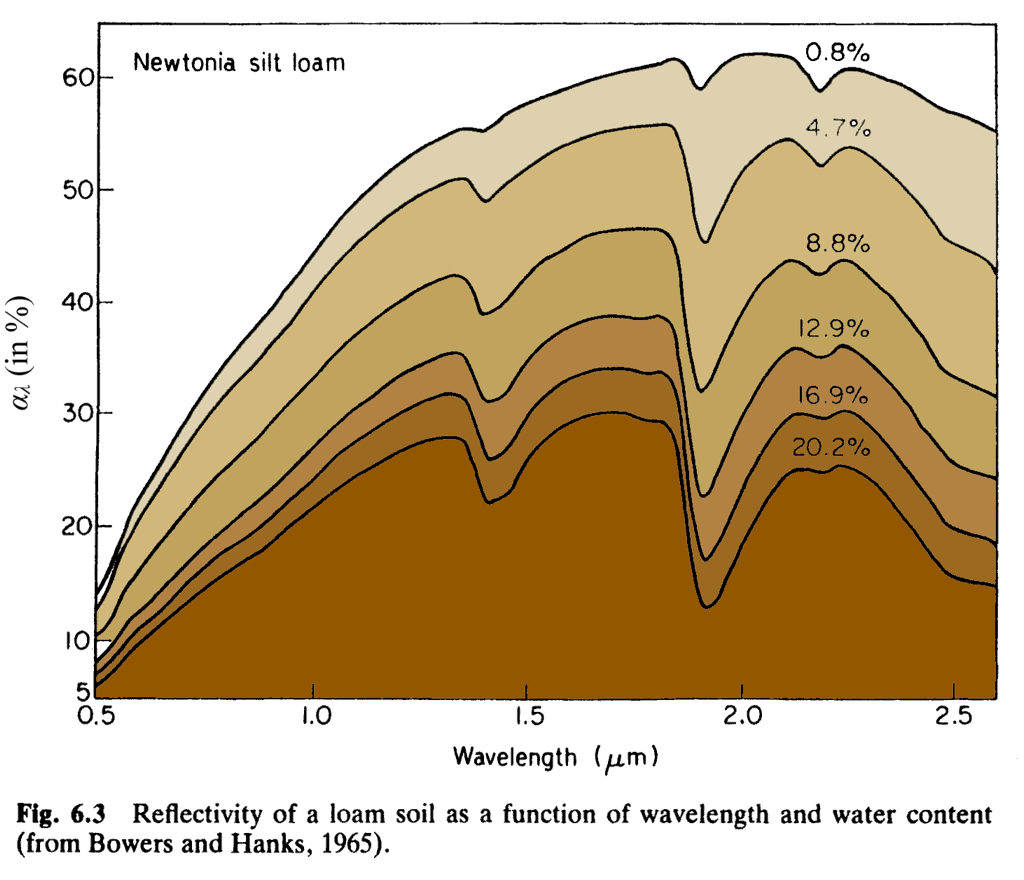
Spectral Reflectivity \(\alpha_{\lambda}\) of Soil

Reflectivity of soil will vary by \(\lambda\) and depend upon its specific composition

• Sand, silt, vs. clay
• Organic content
• Water content

Spectral Reflectivity \(\alpha_{\lambda}\) a Leaf

This is an important diagram that requires some time. Notice the double ended arrow that I have added. It shows a peak in reflection at 0.55 micrometers as well as a peak in transmission at the same wavelength. 0.55 micrometers is the wavelength of GREEN light and explains why leaves appear GREEN to us.

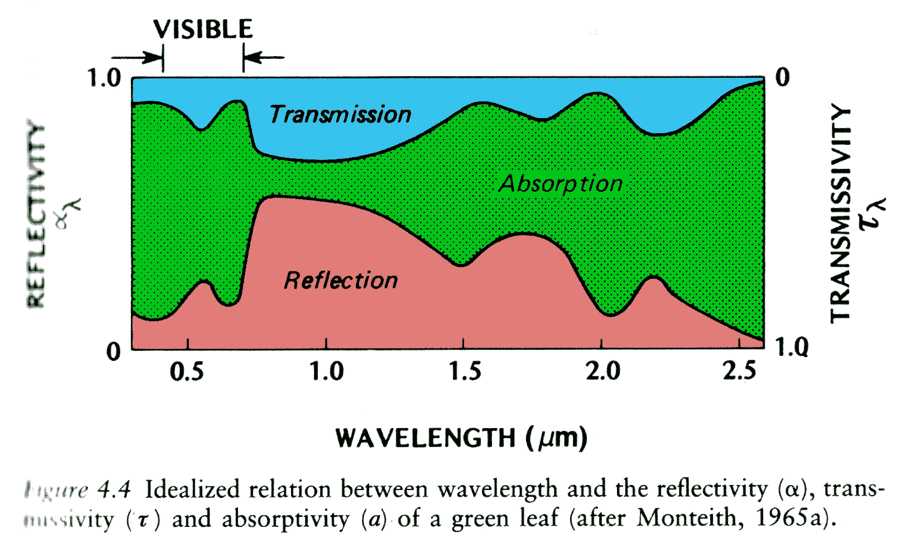
Spectral Reflectivity \(\alpha_{\lambda}\) a Leaf

In the PAR region, \(\alpha_{\lambda}\) and \(\tau_{\lambda}\) are small making \(a_{\lambda}\) large.

• In the NIR region, the opposite is the case
  • The leaf gets rid of radiation that might cause it to get too warm
• The small peaks in \(a_{\lambda}\) and \(\tau_{\lambda}\) at 0.55 \(\mu m\) account for the green color

In the fall leaves change color – WHY?

Test your knowledge (iClicker)

Which leaf has the highest spectral reflectivity at λ = 0.55 \(\mu m\)?

A

B

C

Spectral reflectivity of leaves

Albedo

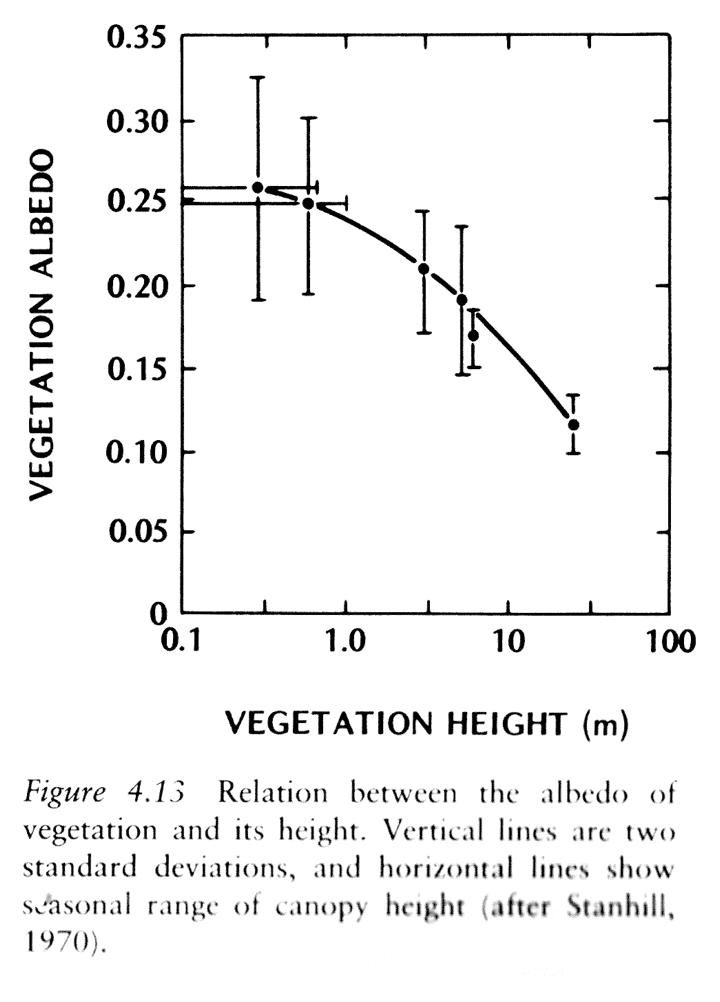
The albedo (\(\alpha_{SW}\)) is calculated as the fraction of incident solar radiation reflected by a surface. Albedo is affected by:

• Angle of incidence
• Plant species
• Leaf development
• Surface wetness
• Surface roughness

Albedo of natural surfaces

• Lowest \(\alpha_{SW}\) (best absorbers)
  • Open water, organic soils, coniferous forest
    • \(\alpha_{SW} \approx\) 0.03 to 0.15
• Intermediate \(\alpha_{SW}\)
  • Deciduous forest
    • \(\alpha_{SW} \approx\) 0.15 to 0.2
  • Agricultural crops
    • \(\alpha_{SW} \approx\) 0.2 to 0.25
• Highest \(\alpha_{SW}\) (poor absorption)
  • Snow, ice, dry light soils, desert sand
    • \(\alpha_{SW} \approx\) 0.35 to 0.95

Test your knowledge (iClicker)

Which system (A or B) has the higher albedo?

Albedo of snow-covered surfaces

Even snow-covered boreal forests have relatively low albedo due to their sides being bare.

Albedo of crops and forests

T.R. Oke (1987): ‘Boundary Layer Climates’ 2nd Edition.

Increased “trapping” of light with increased height. Individual leaves generally have higher reflectivity than a canopy of the same leaves

Take home points

• How does Earth’s geometry, rotation and planetary motion affect the distribution of short-wave irradiance in time and space?
• The reflectivity of soils and vegetation depends greatly on the wavelength of the radiation - giving objects distinct colors and spectral ‘signatures’ useful for remote sensing.
• Albedo = Outgoing reflectance / Incoming irradiance. Key control in the climate system.