Radiation Budget of Planet Earth

The balance of radiative inputs and outputs

Photo from Galileo of the Earth-Moon system in 1992 (NASA)

Photo taken from Apollo 8 astronauts as they orbited the Moon. (Photo: NASA)

Learning Objectives

Because radiation is the only transfer mechanism between our planet and the Sun / Space we can calculate the theoretical radiation budget of Planet Earth.
Know how to estimate the expected ‘temperature’ of our planet based on our calculation.
Understand how the presence of the atmosphere affects the temperature on our planet.

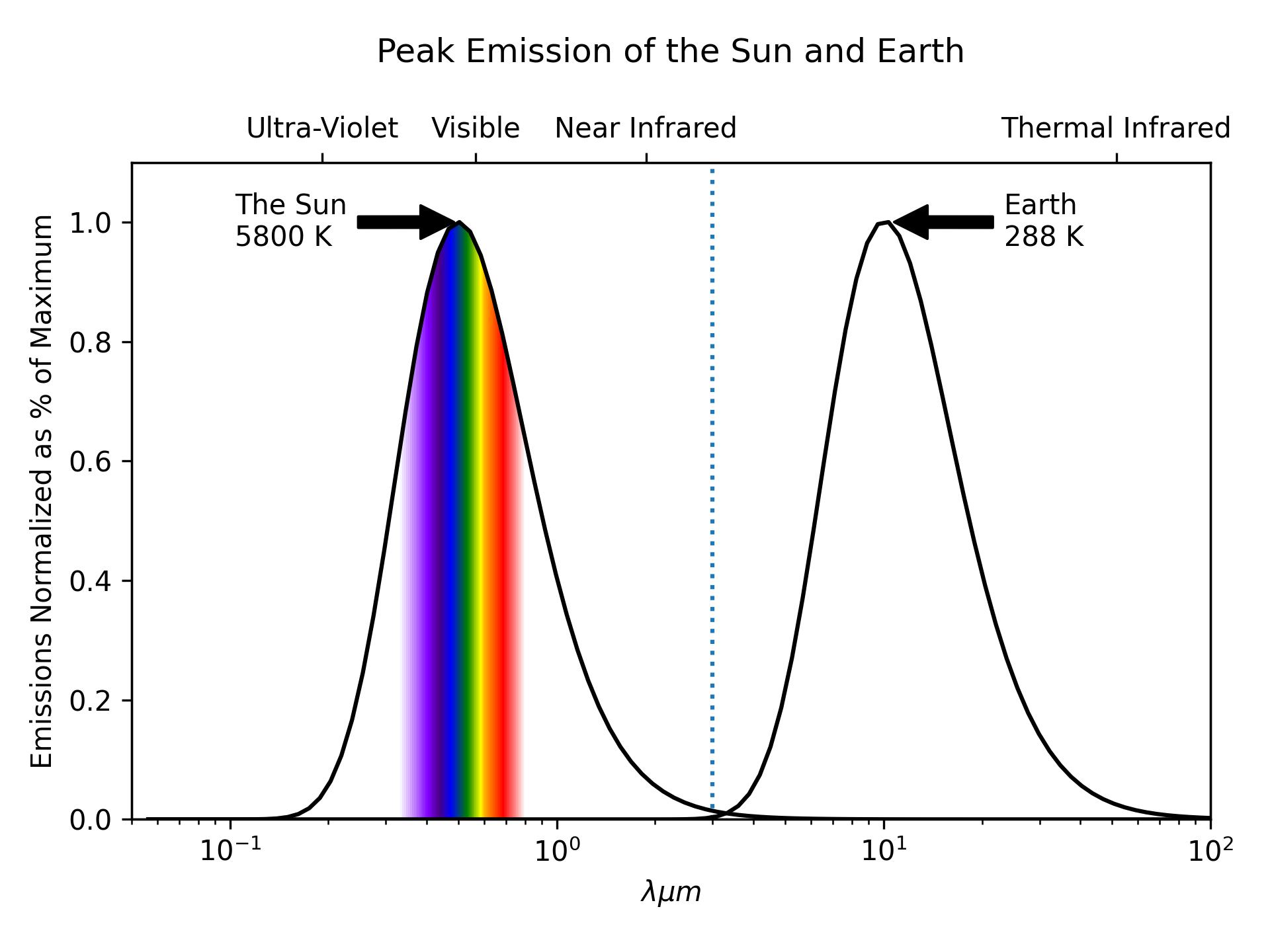
Review ‘Short-wave’ vs. ‘Long-wave’

Short-wave: $\lambda <=3 \mu m$

At 5800 K: $\lambda$ max is 0.50 $\mu m$

Long-wave: $\lambda >3 \mu m$

At 288 K: $\lambda$ max is 10.35 $\mu m$

What is the solar constant $I_0$? (iClicker)

A The average flux density leaving Sun’s surface
B The average flux density reaching the Earth’s surface
C The average flux density reaching the Earth’s orbit perpendicular to the beam
D The average flux density reaching the Earth’s orbit averaged over the sphere of the planet

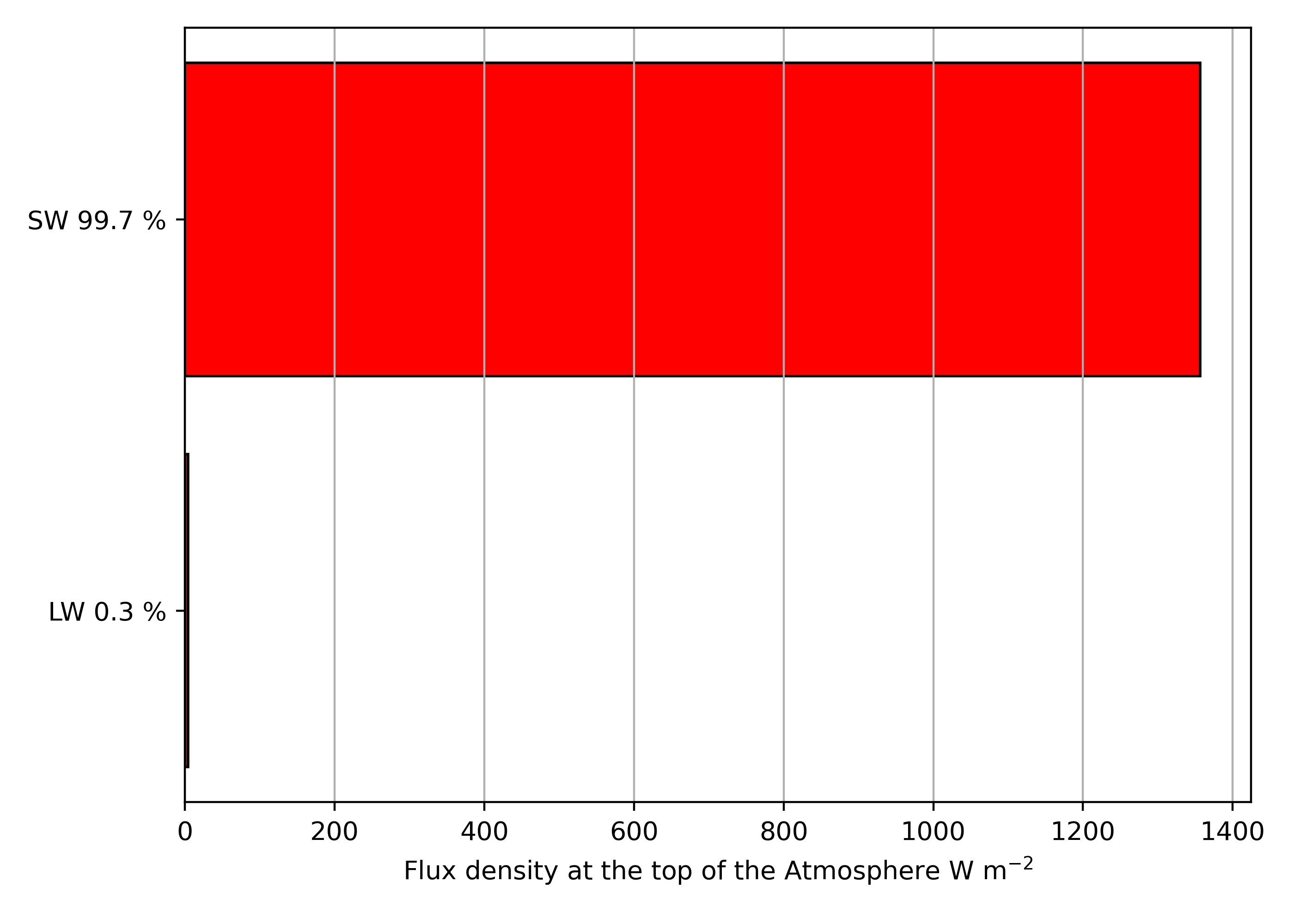
Partitioning the Solar Constant

$I_0 \approx$ 1361 W m^-2.

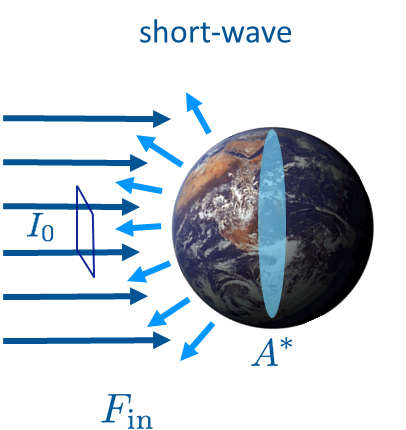
Equilibrium

Earth absorbs incoming $SW$ from the Sun

Earth emits $LW$ to Space

These two fluxes can be considered in equilibrium. Why?
- $F_{in}$ = Short-wave
- $F_{out}$ = Long-wave

Planetary Albedo

Not all $SW$ that reaches a planet from sun is absorbed, a fraction is reflected back to Space.

Planetary albedo $\alpha$: the % of $SW$ reflected back to Space
- $\alpha$ is mainly controlled by:
  - Cloud type/cove
  - Extent of ice and snow
- Earth’s $\alpha$ = 31%

Planetary Absorption

Transmission through Earth is impossible; $a = 1 - \alpha$

Earth’s Albedo: $\alpha \approx 31\%$
- Atmosphere: 22%
  - Clouds, droplets, aerosols
- Surface: 9%
$a = 100\% - 31\% = 69\%$
- Atmosphere: 20%
- Surface: 49%

Planetary Absorption

Recall the solar constant $I_0$: the radiant flux density at the top of the atmosphere perpendicular to the solar beam.

$SW$ Flux into the Earth ($F_{in}$) in W is:

\[ F_{in} = A^*(1-\alpha)I_0 \qquad(1)\]

$I_0$ (W m^-2) projected over Earth’s silhouette area ($A^* = \pi r^{2}$) in m²
- Adjusted for $\alpha$

Planetary Emission

Planetary $LW$ emission ($F_{out}$) in W can be approximated as a function of temperature using Stefan-Boltzmann.

\[ F_{out} = AI_{out} = 4\pi R^{2}\epsilon\sigma_b T^4 \qquad(2)\]

Average flux density ($I_{out}$) in W m^-2 times Earth’s surface area
- $\epsilon_{surface} \approx 0.95$
- $T \approx 288 K$

Surface Emissivity

Simplified Energy Balance:

Let us assume an equilibrium state, i.e. $F_{in} = F_{out}$

\[ \pi R^{2} (1-\alpha)I_0 = 4\pi R^{2}\epsilon\sigma_b T^4 \qquad(3)\]

Outgoing $LW$ will balance out incoming $SW$

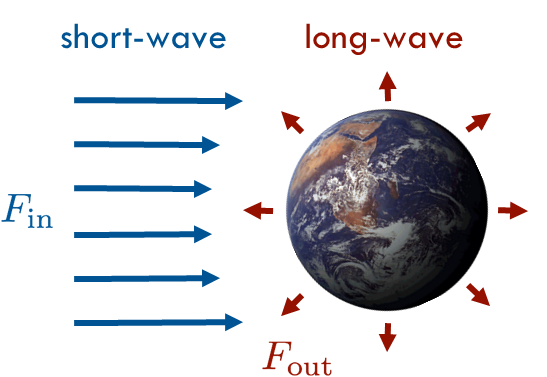
Geometric Considerations

Earth receives $SW$ only from ‘one side’; but emits $LW$ in all directions to space.

$F_{in}$ is distributed over the silhouette area $A^*$ of Earth
$F_{out}$ is from the whole surface area $A$ of Earth
- Note $F_{out}$ is not constant across space

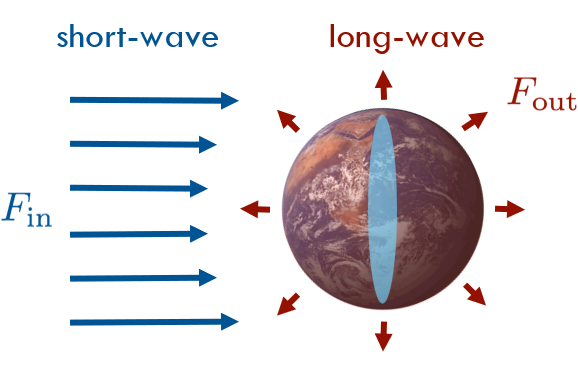
Earth’s Surface Temperature (iClicker)

The area terms ($\pi R^2$) in Equation 3 cancel on both sides; leaving us with

$(1-\alpha)I_0 = 4\epsilon\sigma_b T^4$

Rearranging to solve for T:

$T = \sqrt[4]{\frac{(1-\alpha)I_0}{4\epsilon\sigma_b}}$

I0 <- 1361 # W m-2
alpha <- 0.31
epsilon <- 0.95
sigma <- 5.67e-8 # W m-2 K-4

T = ((1-alpha)*I0/(4*epsilon*sigma))**.25

$T \approx$ 256.9 K

Is this value realistic?

A - Yes
B - No (underestimate)
C - No (overestimate)

Effect of an atmosphere

Earth’s known average surface temperature is 15 ° C.

The previous calculation underestimates surface temperature because we have not incorporated the atmosphere i.e. the effects of greenhouse gases.
Without an atmosphere it would be $T \approx$ -16.2 ° C on Earth on average.
- The effect of the atmosphere (natural greenhouse effect) must be worth $\approx$ 31.2 K!

The ‘Greenhouse Effect’

The atmosphere has an insulating effect on planet earth.

The greenhouse gas effect limits the $\tau_{LW}$ through the atmosphere
- This effectively reduces Earth’s $\epsilon_{LW}$
- But how? Kirchhoff’s law states that $\epsilon_{\lambda} = a_{\lambda}$?
The $a_{LW}$ is re-emitted in all directions
- i.e., it is recycled
- Loss of energy from the surface slowed

The ‘Greenhouse Effect’

The atmosphere is a selective absorber (and emitter) of radiation.

The transmission window allows some $LW$ through
Outside of that window, little $LW$ escapes!

The Effective Emissivity

Since we know the mean surface temperature of the earth, we can instead rearrange Equation 3 to solve for $\epsilon$:

$\epsilon= \frac{(1-\alpha)I_0}{4\sigma_bT^4}$

I0 <- 1361 # W m-2
alpha <- 0.31
T_s <- 15 # C
sigma <- 5.67e-8 # W m-2 K-4

T = T_s + 273.15

epsilon = (1-alpha)*I0/(4*sigma*T**4)

The atmosphere reduces the global value of $\epsilon$ to $\approx$ 0.601

Radiative Output

Since we now have a reasonable estimate of $\epsilon$, we estimate planetary emissions following Equation 2.

$F_{out} = AI_{out} = 4\pi R^{2}\epsilon\sigma_b T^4$

I_out = epsilon*sigma*T**4

R = 6378.1 # km
R = R * 1000

F_out = 4*pi*R**2*I_out

The average flux density of $LW$ at the top of Earth’s atmosphere $I_{out} \approx$ 234.8 W m^-2

The average flux of $LW$ from Earth $F_{out} \approx$ 1.2001616^{17} W

Radiative Output (iClicker)

Our estimated value of $I_{out}$ (234.8 W m^-2) $\neq I_0$ (1361 W m^-2).

What accounts for the discrepancy?

A - $I_0$ is distributed across Earth’s silhouette area $A^*$; we need distribute $I_0$ across Earth’s total surface area $A$

B - A portion of $I_0$ is never absorbed by the Earth due to the planetary Albedo ($\alpha \approx 0.31$)

C - Both A & B

Radiative Output

If we account for both, we’ll get the average flux density at the top of Earth’s Atmosphere across the Full electromagnetic spectrum.

$\bar{I_0} = \frac{I_0}{4}$ = 340.25 W m^-2
$\bar{I_0}= \bar{I_0} \alpha + I_{out}$ = 105.4775 W m^-2 + 234.7725 W m^-2

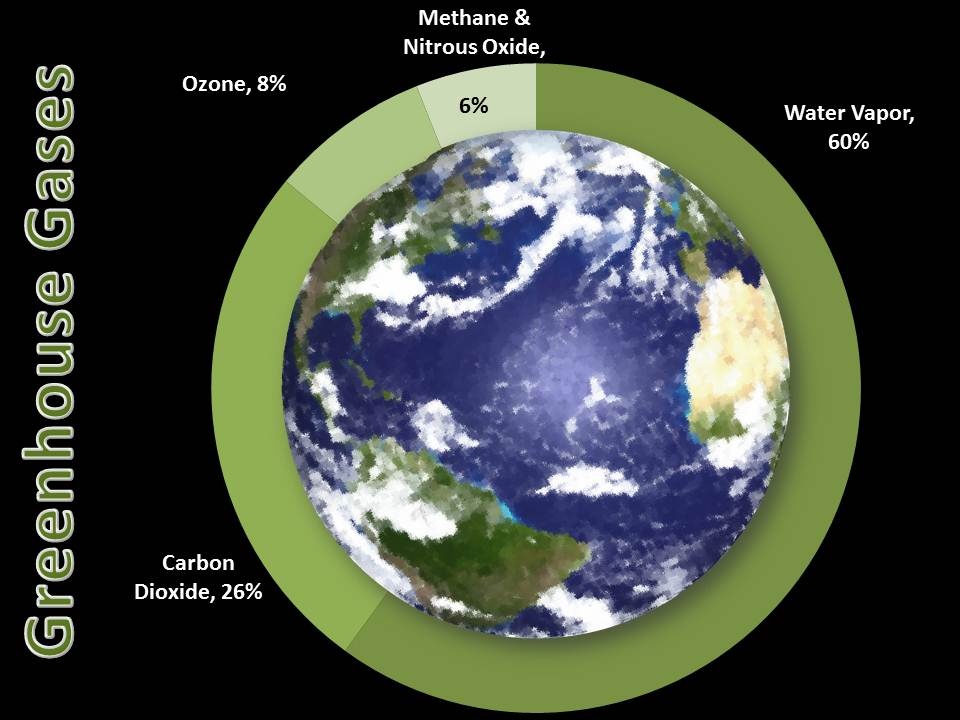
Important greenhouse gases

Table 1: Includes other trace gases (halocarbons, not shown)
Compound	Abundance pre industrial	Abundance 2011	Lifetime yr	Effect of human enhancement
H₂O	Variable	Variable	0.03	—
CO₂	~280 ppm	393 ppm	5 - 200	1.85 W m-2
CH₄	~700	1874 ppb	12	0.51 W m-2
N₂O	~270	324 ppb	114	0.18 W m-2
Ozone O₃	25 ppm	34 ppm	days	0.35 W m-2
Misc. Trace Gasses				0.34 W m-2 *
All				3.23 W m-2

Test your knowledge (iClicker)

What is the most important greenhouse gas contributing to the natural greenhouse effect on our planet?

A Ozone
B Carbon dioxide
C Methane
D Oxygen
E Water vapour

Test your knowledge

What is the most important greenhouse gas contributing to the natural greenhouse effect on our planet?

A more Realistic Energy Balance

Magnitudes from Kiehl and Trenberth (1997, Bull. Am. Met. Soc.) in IPCC 2001.

There is no net gain or loss for Earth

$SW$ input (100%) = $SW$ loss (31%) + $LW$ (69%):

$I_{0} = \bar{I_0} \alpha + I_{out}$

Magnitudes from Kiehl and Trenberth (1997, Bull. Am. Met. Soc.) in IPCC 2001.

Energy Balance of the Atmosphere

The Atmosphere appears to be in radiative deficit
- Should be cooling
The surface in radiative surplus
- Should be warming
Why is this not happening?

Energy Balance of the Atmosphere

Earth’s surplus is convected by sensible and latent heat flux into the Atmosphere
- Offsets the radiative imbalance,
- i.e. the whole energy balance is involved not just radiation

Latent Heat Flux (iClicker)

How is a latent heat flux into the Atmosphere realized?

A - Water is vaporized by radiation at the surface and condenses in clouds - there it warms up air.
B - Radiation absorption at surface warms up air near surface - warm air rises and transports extra heat to higher layers of atmosphere.
C - Rain releases its geopotential energy as raindrops splash at the surface - they warm up the surface more than the atmosphere.

Take home points

The planet is using (absorbing) only 69% of the solar radiation received. The planetary albedo is 31%.
Without atmosphere it would be -16.5579764$° C on Earth on average. The natural greenhouse effect is worth -31.2 K.
The atmosphere is in a radiative deficit and the Planet’s surface shows a radiative surplus. Sensible and latent heat fluxes offset the radiative imbalance, i.e. transport energy from the surface into the atmosphere.

Radiation Budget of Planet Earth

Learning Objectives

Review ‘Short-wave’ vs. ‘Long-wave’

What is the solar constant \(I_0\)? (iClicker)

Partitioning the Solar Constant

Equilibrium

Planetary Albedo

Planetary Absorption

Planetary Absorption

Planetary Emission

Surface Emissivity

Simplified Energy Balance:

Geometric Considerations

Earth’s Surface Temperature (iClicker)

Effect of an atmosphere

The ‘Greenhouse Effect’

The ‘Greenhouse Effect’

The Effective Emissivity

Radiative Output

Radiative Output (iClicker)

Radiative Output

Important greenhouse gases

Test your knowledge (iClicker)

Test your knowledge

A more Realistic Energy Balance

There is no net gain or loss for Earth

Energy Balance of the Atmosphere

Energy Balance of the Atmosphere

Latent Heat Flux (iClicker)

Take home points