Atmospheric Environments - Heat and temperature

Learning Objectives

Understand the linkage between temperature and life.

Describe what determines the temperature response to an energy input.
Explain why soils warm and cool differently and how this is related to the role of water content.

Temperature and life-forms

Temperature has a major effect on various life forms.
Temperature limits growth, reproduction and survival of a species.

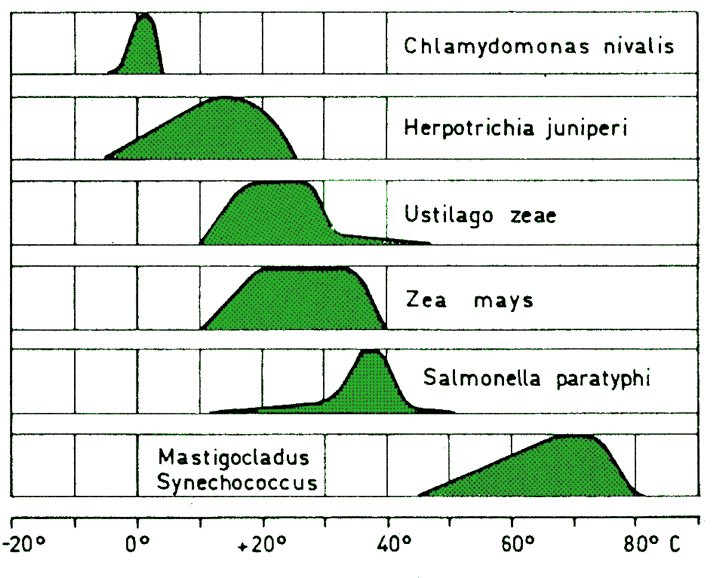
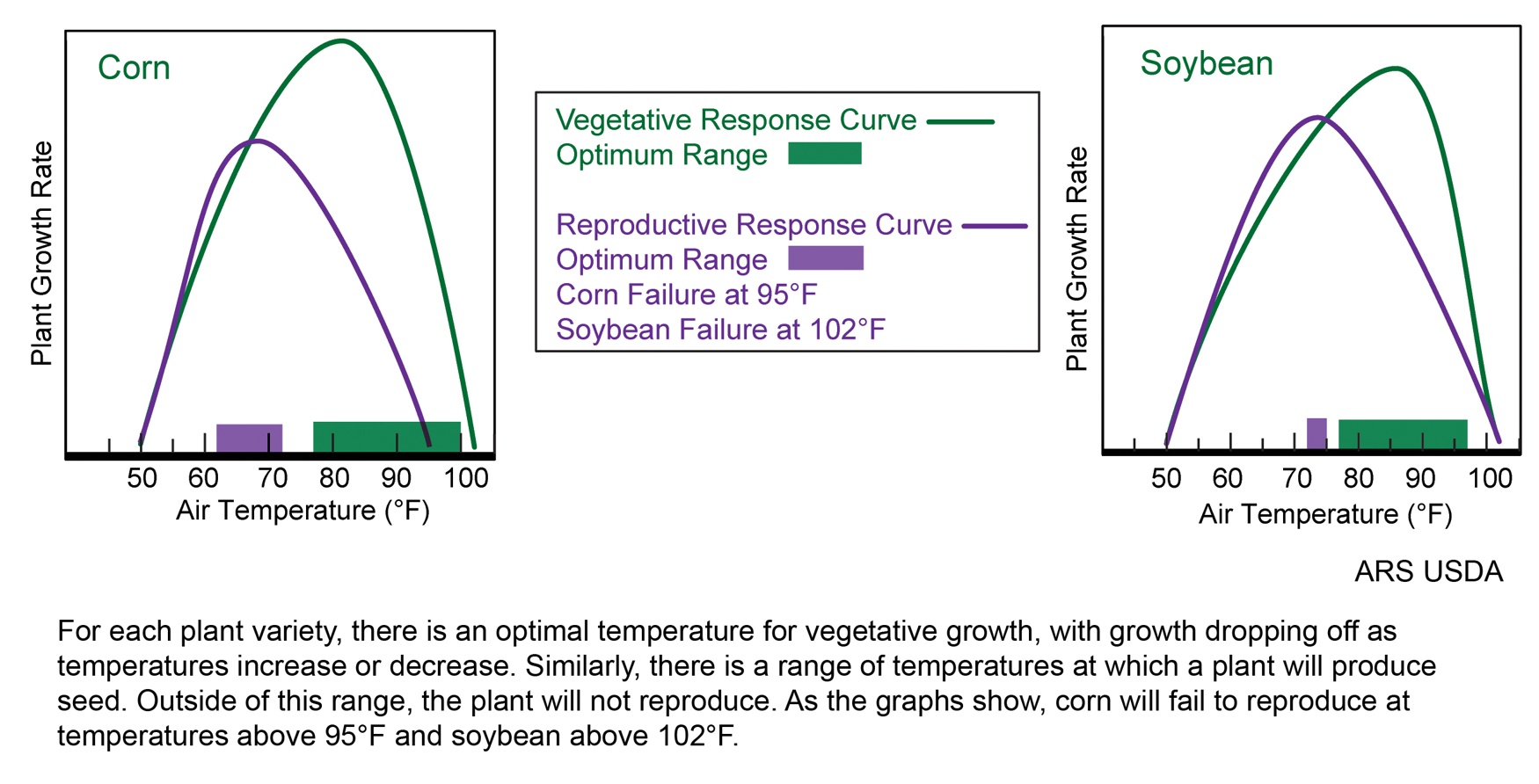
Optimal temperature ranges for various lifforms

Temperature and plant growth

Surface and soil temperatures can be a risk for plants, hence there are several practices aimed to reduce heat or frost stress.

Here we look at the processes controlling soil temperatures to understand soil climates and design better practices for plant growth.

Spruce seedlings in controlled temperature experiment

Temperature and plant growth rate

Soil climates

Soil temperatures are controlled by available energy

Varies with latitude and proximity to the coast in BC
Also influenced by topography, soil type, and moisture
- Abbotsford 11 °C
- Prince George 6.4 °C

Figure 1: Average soil temperature by month.

Heat vs. Temperature

Heat: is thermal energy.

Travels from hotter to colder objects
Can do work
Often expressed in Joules (J)
- J = 1 N x 1 m
- Newton (N) = 1 kg m s^-2

Temperature a (relative) measure of thermal energy.

Increases/decreases when heat is added/removed
Cannot do work
Expressed in Kelvin (K)
- Or Celsius (C)

Heat vs. Temperature

During phase changes, heat is added to a substance, but the temperature does not change.

Recall - Fluxes and flux densities

Heat

Aka. Energy
- J (Joules)

Heat Flux

Flow rate of energy
- Aka. Power
- W = J s^-1

Heat Flux Density

Net transfer of energy
- Flow rate of energy per unit area
- W m-2 = J s^-1 m^-2

Heat Capacity

Heat capacity (\(C\)) is the quantity of heat required to raise the temperature of a unit volume (e.g., 1 m^-3) of a material 1 K.

Table 1: Heat capacity of various substances
Material	Heat capacity MJ m^-3 K
Air	0.0012
Water (liquid)	4.1800
Ice	1.9000
Soil mineral	2.1000
Soil organic matter	2.5000
Wood organic matter	2.0000

Test your knowledge (iClicker)

You run an experiment using a camping stove with a 1 liter pan to heat up four different substances. You run the stover for the same amount of time (1 minute) and use the same volume of each substance (exactly 1 liter). All substances start at the same temperature (15 \(^{\circ} C\)); which substance will have the highest temperature at the end of the 1 minute period?

A Water
B Air (empty pan with lid)
C Dry Soil
D Food in water (e.g. rice)

Specific Heat

Specific heat \(c\) is the quantity of heat required to raise the temperature of a unit mass (e.g., 1 Kg) of a material 1 K.

Table 2: Specific heat of various substances
Material	Specific heat kJ kg^-1 K^-1
Air	1.01
Water (liquid)	4.18
Ice	2.10
Soil mineral	0.80
Soil organic matter	1.90
Wood organic matter	1.30

What is the relationship between \(C\) and \(c\) ?

Density (\(\rho\)) of the material:

\[ C=\rho c \qquad(1)\]

Example of water:

\(C =\) 1 Mg m^-3 \(x\) 4.18 J kg^-1 K^-1 =
4.18 J⁶ m^-3 K^-1 = 4.18 MJ m^-3 K^-1

Table 3: Density heat of various substances
Material	Density Mg m^-3
Air	0.0012
Water (liquid)	1.0000
Ice	0.9000
Soil mineral	2.6500
Soil organic matter	1.3000
Wood organic matter	1.5000

Why is this important?

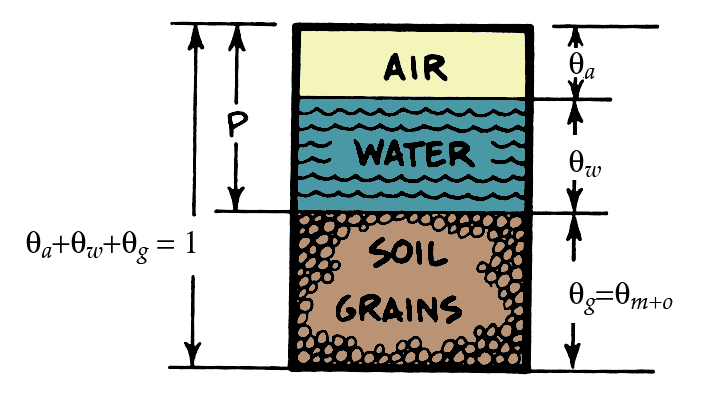
Porosity & volume fractions \(\theta\) will dictate heat capacity of soil

Compound Substances

The heat capacity of a mixture of substances can be calculated from the heat capacity and volume fraction of each component. For soil:

\[ C_{soil}=C_{m}\theta_{m}+C_{o}\theta_{o}+C_{w}\theta_{w}+C_{a}\theta_{a} \qquad(2)\]

\(\theta\) is the volume fraction of mineral (m), organic matter (o), water (w) and air (a)
- Note: \(C_a\) is very small relative to the other values of C

The role of soil moisture

Table 4: Heat capacity of various substances
Material	Heat capacity MJ m^-3 K
Air	0.0012
Water (liquid)	4.1800
Ice	1.9000
Soil mineral	2.1000
Soil organic matter	2.5000
Wood organic matter	2.0000

Heat capacity Soils

We have a soil that is 45% minerals and 0% organic matter by volume. The rest is pore space (for air or water).

Dry Mineral Soil

C_w = 4.18
C_m = 2.1
C_o = 2.5
C_a = 0.0012
theta_m = .45
theta_o = 0
theta_w = 0
theta_a = 1-(theta_w+theta_o+theta_m)
C_dry_mineral = C_m*theta_m+C_o*theta_o+C_w*theta_w+C_a*theta_a

\(C =\) 0.94566 MJ m^-3 K^-1

Saturate Soil

theta_a = 0
theta_w = 1-(theta_a+theta_o+theta_m)
C_saturated_mineral = C_m*theta_m+C_o*theta_o+C_w*theta_w+C_a*theta_a

\(C =\) 3.244 MJ m^-3 K^-1

Heat capacity Soils (iClicker)

We have a soil that is 0% minerals and 45% organic matter by volume and 25% water by volume. What would it’s heat capacity be in MJ m^-3 K^-1?

Wet (not saturated) Organic Soil

C_w = 4.18
C_m = 2.1
C_o = 2.5
C_a = 0.0012
theta_m = 0
theta_o = .45
theta_w = .25
theta_a = 1-(theta_w+theta_o+theta_m)
C_wet_organic = C_m*theta_m+C_o*theta_o+C_w*theta_w+C_a*theta_a

A 2.17036 MJ m^-3 K^-1
B 0.94566 MJ m^-3 K^-1
C 3.244 MJ m^-3 K^-1

\(C =\) 2.17036 MJ m^-3 K^-1

Heat Capacity

Organic soils usually have high porosity, so they can hold more water so more heat is required to warm them compared to mineral soils.

Table 5: Heat capacity of natural materials
Mixture	% H2O content	Density(Mg m^-3)	Heat capacity C(MJ m^-3 K^-1)
Mineral soil (dry / saturated)	0 / 0.55	1.20 / 1.75	0.90 / 3.2
Wood (dry / saturated)	0 / 0.60	0.60 / 1.20	0.80 / 3.3
Peat soil (dry / saturated)	0 / 0.85	0.20 / 1.05	0.40 / 3.9
Animal / plant tissue	~0.9	1.1	3.7

Heat Capacity of Soils

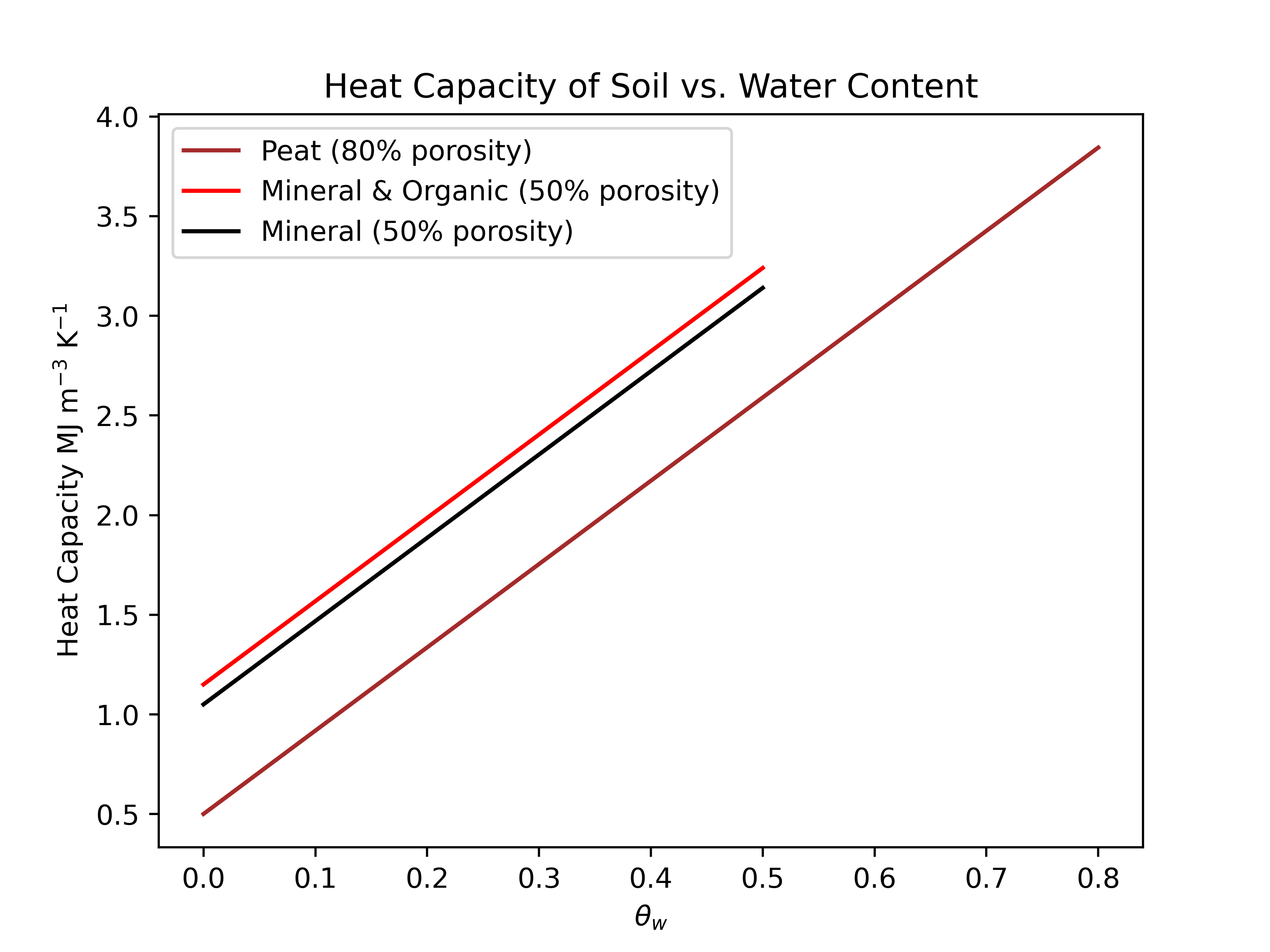
Porosity & saturation are the a dominant controls, mineral vs. organic is secondary

Soil Heat Flux (\(H_g\))

Describes the transfer of heat through a volume of soil.

The heat flux (\(H_g\)) through a soil layer of depth \(z\), is proportional to the rate of soil temperature change (\(\Delta T_s\)) of time \(t\) and the heat capacity (\(C\)) of the soil.

\[ \frac{H_g}{z} = C \frac{\Delta T_s}{t} \qquad(3)\]

Heat Fluxes and Thermal Effects

Positive indicates a surplus of energy at the surface being transferred downwards through the soil via conduction. Negative indicates a surplus at depth being transferred upwards through the soil via conduction.

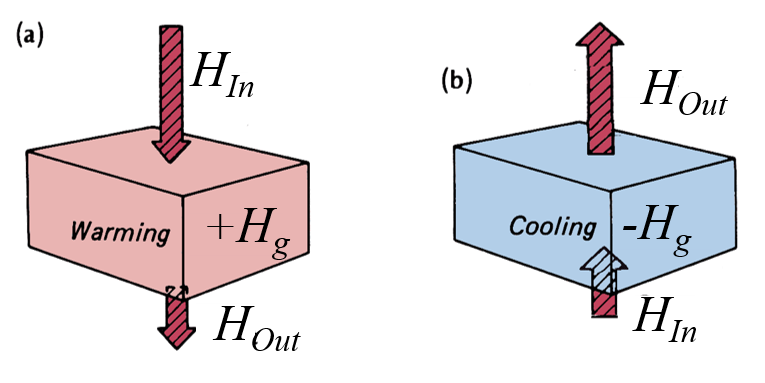
a. During day, positive heat flux warms the soil b. At night, negative heat flux cools the soil

Heat Fluxes and Net Radiation

\(H_g\) will be correlated with \(R_n\), though its not a direct relationship, and the strength of the relationship will vary by site conditions.

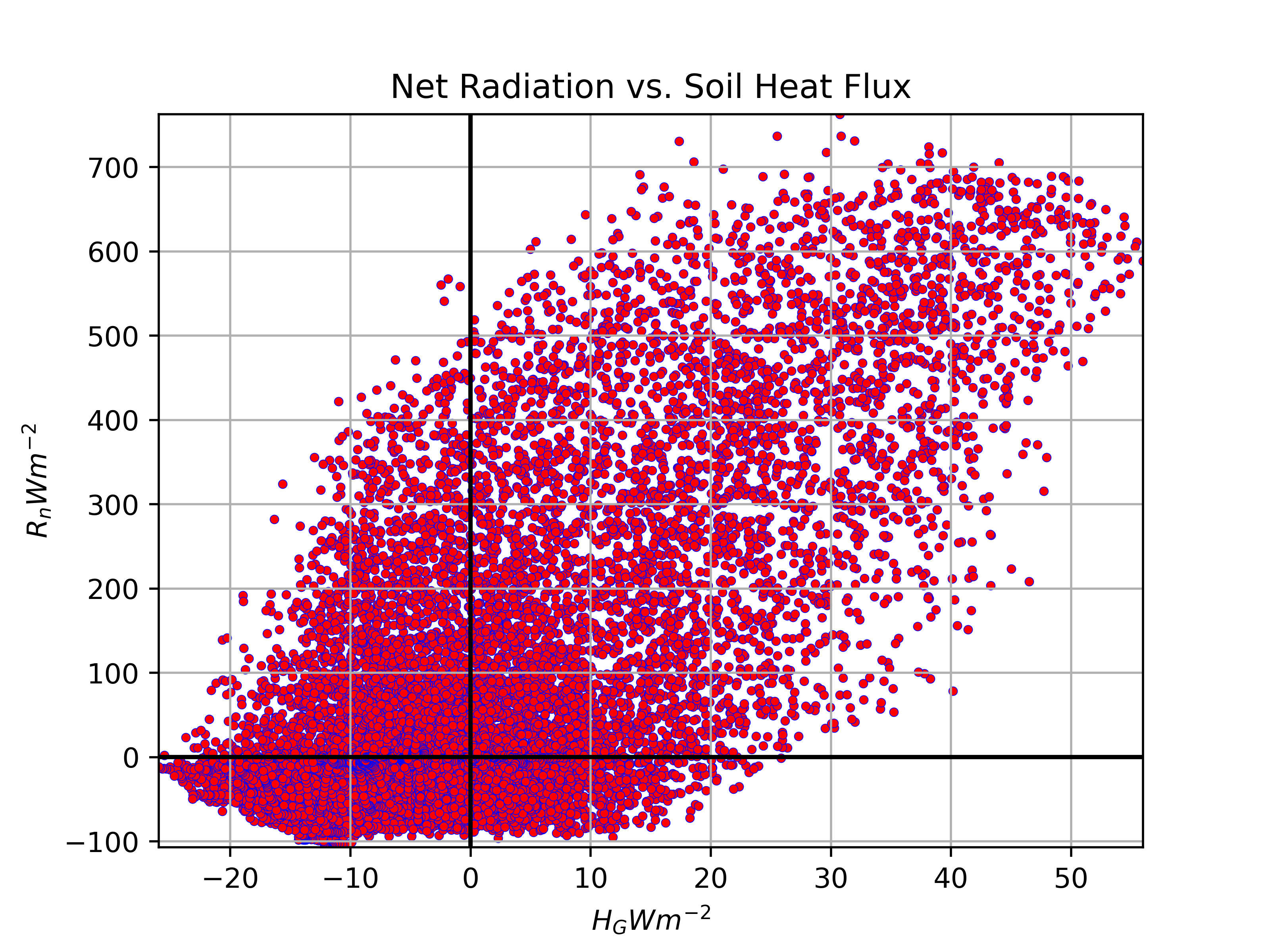
Net radiation (\(R_n\)) and soil heat flux (\(H_g\)) at the Burns Bog EC station, 2022

Warming / cooling rates

The higher C, the smaller the rate of temperature change.

A wet soil (high \(C\)) heats/cools slowly.

A dry soil (low \(C\)) is heats/cools rapidly.

Test your knowledge (iClicker)

Given same amount of energy input by radiation (e.g. same day), which soil will warm up more rapidly? The photos show the same location:

How fast does a moist soil warm up?

We have a mineral soil with \(\approx\) 30% water content by volume, giving it C = 2 MJ m^-3 K^-1. With a soil heat flux (H) of 100 W m^-2 going into the soil surface layer of depth z = 0.1 m. Rearranging Equation 3 we can solve for \(\Delta T\):

\(\frac{\Delta T}{t} = \frac{1}{C}\frac{H_g}{z}\)

\(\frac{\Delta T}{t} = \frac{1}{2 MJ m^{-3} K^{-1}}\frac{100 J m^{-2} s^{-1}}{0.1 m}\)

0.0005 K s^-1 = 1.8 K H^-1

Test your knowledge (iClicker)

You run an experiment using camping stove with a 1 liter pan to heat up four different substances. You run the stover for the same amount of time (1 minute) and use the same volume of each substance (exactly 1 liter). All substances start at the same temperature (15 \(^{\circ} C\)); which substance will have the lowest temperature at the end of the 1 minute period?

A Water
B Air (empty pan with lid)
C Dry Soil
D Food in water (e.g. rice)

Take home points

Plant growth is determined by surface and near-surface soil temperatures.
- In Agriculture and forestry, there is potential to manage soil temperatures.
Heat capacity \(C\) and specific heat \(c\) are linked by density.
Temperature change in the soil controlled by soil heat capacity.
Important role of soil volumetric water content for temperature changes - quick dry soils vs. slow wet soils.